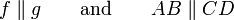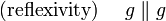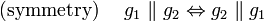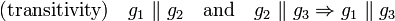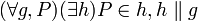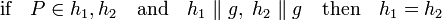Parallel (geometry)
According to the common explanation two straight lines in a plane are said to be parallel (or parallel to each other) if they do not meet (or intersect), i.e., do not have a point in common. The term parallel is also used for line segments that are part of parallel lines.
This definition is correct if (silently) the "natural" (Euclidean) geometry is assumed.
In it, the explicit condition "in a plane" is necessary because in space two straight lines that do not intersect need not be parallel.
Non-intersecting lines that do not belong to a common plane are called skew.
Important properties of the notion "parallel" in Euclidean geometry are:
- (Uniqueness) Given a line then through any point (not on it) there is a uniquely determined line parallel to the given one.
- (Equidistant lines) Parallel lines have constant distance.
(This means, more precisely, that all distances from a point on one of them to the other line are the same.) - (Transitivity) If among three distinct lines two pairs of lines are parallel then the third pair is also parallel.
Generalizations:
- Analoguously, in three-dimensional space two planes, or a line and a plane, are said to be parallel if they do not intersect.
In this case, no additional condition is necessary because they always belong to the "same space". (This is different, of course, if, more generally (hyper-)planes in higher-dimensional spaces are considered.)
[edit] Mathematical significance
The statement that on a plane, to a straight line, there is only one parallel through a point plays an important role in the development of geometry and mathematics in general. Euclid states it — somewhat disguised — in his Elements as his fifth (and last) postulate. Therefore it is usually called the Parallel Postulate or Parallel Axiom.
Since this statement is much less natural or evident than Euclid's other axioms and postulates, mathematicians of all periods tried to prove it from the other assumptions, but in vain. Only as late as the nineteenth century the reason became clear, namely, that it can be neither proven nor disproven (Details). The statement is independent of the other axioms.
This discovery led to the development of an alternative geometry, that of the non-Euclidean or hyperbolic plane in which, to a given line and a point not on the line, there are infintely many non-intersecting lines through this point. Among these lines — usually also called parallels — there are two boundary lines — called horoparallel (also limiting, asymptotically or critically parallel) — that enclose the other parallels called hyperparallel (or ultra-parallel). Some authors reserve the word "parallel" for the two exceptional lines.
While Newton's classical mechanics is based on Euclidean geometry, Einstein's relativity theory showed that physical space — while locally Euclidean — is not Euclidean in the large.
[edit] Mathematical properties
In mathematical formulas, "is parallel to" is usually denoted by the symbol ∥ (Unicode U+2225) — two parallel vertical lines — and its negation "is not parallel to" by ∦ (Unicode U+2226).
Thus, for two straight lines f and g, and for four points A,B,C,D
mean that the lines f and g, and the line segments determined by AB and CD, respectively, are parallel.
[edit] Binary relation
The relation 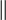 is a binary relation on the set of straight lines.
is a binary relation on the set of straight lines.
In mathematics, it is usual to define — in addition to the common meaning — that any line is parallel to itself.
This convention is convenient in the following statements (transitivity, parallel through a point).
The relation 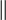 is an equivalence relation:
is an equivalence relation:
The Parallel Axiom consists of the following two statements:
- For all points P and all lines g there is a parallel line h through P:
and
- Any two lines parallel to g and through P are the same:
These statements remain true if (instead of straight lines) line segments, or planes are considered.
However, transitivity and the uniqueness of a parallel fail when lines and planes are considered simultaneously.
They also fail in the non-Euclidean case, of course.
| |
Some content on this page may previously have appeared on Citizendium. |