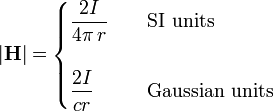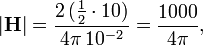Oersted (unit)
In physics, the oersted (symbol Oe) is the unit of magnetic field strength |H| in the emu (electromagnetic unit) and Gaussian systems of units. Both systems are cgs (centimeter-gram-second) systems.
The relation to the corresponding SI unit (ampere times turn per meter) is
- 1 Oe =
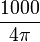 A⋅turn/m.
A⋅turn/m.
See solenoid for the explanation of the SI unit, which is one of the few electromagnetic units that carries no name.
The oersted is named for the Danish scientist Hans Christian Oersted.
[edit] Definition
The definition of Oe follows from the Biot-Savart law giving the magnetic field strength field |H| due to an electric current I in an infinitely long straight conductor,
where r is the distance of the field point to the conductor and c is the speed of light (≈ 3⋅1010 cm/s). In the SI definition r is in meters, whereas in Gaussian units r is in centimeters.
For Gaussian units, the oersted is defined as the strength of the magnetic field at a distance of 1 centimeter from a straight conductor of infinite length and negligible circular cross section that carries a current of ½⋅c statA (statampere).
[edit] Conversion to SI units
Because the speed of light c in two different units is needed, it will be written numerically—but approximately—as 3·108 m/s (SI) or 3·1010 cm/s (cgs). Since only the ratio (exactly 100) is needed, the end result is exact.
In order to explain the factor 1000/4π, relating Oe (Gaussian) and A⋅turn/m (SI), consider an infinite wire carrying a current of ½⋅3⋅1010 statA and measure |H| at one cm distance from the wire. By definition the field has the strength 1 Oe. Noting that 1 statA = 1 A/(10⋅c), the current is equal to
- I = ½⋅3⋅1010 statA = ½⋅3⋅1010 A/(3⋅109) = ½⋅10 A,
Applying the Biot-Savart equation valid in SI units (current I in A, distance r in m), we find that the field in the same physical setup, but expressed in A⋅turn/m is
from which follows that a field of strength 1 Oe has strength 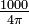 A·turn/m exactly. Since "turn" (number of turns) is a dimensionless number, it is often omitted in the SI unit, which then becomes simply A/m.
A·turn/m exactly. Since "turn" (number of turns) is a dimensionless number, it is often omitted in the SI unit, which then becomes simply A/m.
[edit] Notes
1. Before 1930 there was much confusion about the difference between the gauss (the Gaussian unit of magnetic flux density B) and the oersted. At its meeting in Stockholm in 1930 the Advisory Committee on Nomenclature of the International Electrotechnical Commission eliminated all ambiguity by adopting the gauss for the unit of magnetic flux density and the oersted for the unit of magnetic field strength. The gauss is defined through a time-dependent change in magnetic flux density and the oersted is defined through the field created by an electric current.
2. The historically oldest definition of the oersted is: The magnetic field strength |H| in a point in vacuum is 1 Oe, if a unit magnetic pole in the point experiences a force of 1 dyne ( = 1⋅10−5 newton). Because a magnetic pole does not exist in nature and must be realized by a long bar magnet, this definition was not practicable and is now obsolete.