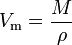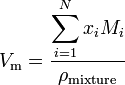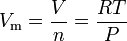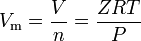Molar volume
The molar volume (symbol Vm) of a substance is the volume occupied by one mole of the substance at a given temperature and pressure.[1][2] It is equal to the molecular mass (M) of the substance divided by its density (ρ) at the given temperature and pressure:
It has an SI unit of cubic metres per mole (m3/mol).[1][2] However, molar volumes are often expressed as cubic metres per 1,000 moles (m3/kmol) or cubic decimetres per mol (dm3/mol) for gases and as centimetres per mole (cm3/mol) for liquids and solids.
If a substance is a mixture containing N components, the molar volume is calculated using:
where x i is the mole fraction of the ith component, M i is the molecular mass of the ith component and ρmixture is the mixture density at the given temperature and pressure.
When stating molar volume numerical values, it is important to also state the given conditions of temperature and pressure. Otherwise, the numerical values are meaningless.
[edit] Ideal gases
The ideal gas law equation can be rearranged to give this expression for the molar volume of an ideal gas:
Where in SI units:
| P | = the gas absolute pressure, in Pa |
|---|---|
| n | = number of moles, in mol |
| Vm | = the gas molar volume, in m3/mol |
| T | = the gas absolute temperature, in K |
| R | = the universal gas law constant of 8.314472 m3·Pa·mol-1·K-1 |
Where in U.S. customary units:
| P | = the gas absolute pressure, in psia |
|---|---|
| n | = number of moles, in lb-mol |
| Vm | = the gas molar volume, in ft3/lb-mol |
| T | = the gas absolute temperature, in degrees Rankine (°R) |
| R | = the universal gas law constant of 10.7316 ft3·psia·lb-mol-l·°R-1 |
Example calculations of ideal gas molar volumes:
- In SI metric units:
- Vm = 8.314472 × 273.15 / 101,325 = 0.022414 m3/mol at 0 °C and 101,325 Pa absolute pressure = 22.414 m3/kmol at 0 °C (273.15 K) and 101.325 kPa absolute pressure
- Vm = 8.314472 × 273.15 / 100,000 = 0.022711 m3/kmol at 0 °C and 100,000 Pa absolute pressure = 22.711 m3/kmol at 0 °C (273.15 K) and 100 kPa absolute pressure
- In customary USA units:
- Vm = 10.7316 × 519.67 / 14.696 = 379.48 ft3/lb-mol at 60 °F (519.67 °R) and 14.696 psia
Notes:
- lb-mol is an abbreviation for pound-mol
- °R is degrees Rankine (an absolute temperature scale) and °F is degrees Fahrenheit (a temperature scale).
- °R = °F + 459.67
- The technical literature can be confusing because some authors often fail to explain whether they are using the universal gas law constant R, which applies to any ideal gas, or whether they are using the specific gas law constant Rs, which only applies to a specific individual gas. The relationship between the two constants is Rs = R / M where M is the molecular mass of the gas.
[edit] Real gases
Real gases are those gases that do not exhibit ideal gas behavior. For such gases, the simplest method of determining molar volumes is by using compressibility factors as in the following expression:
where Z is the gas compressibility factor, which is a useful thermodynamic property for modifying the ideal gas law to account for behavior of real gases.[3] The above equation is basically a simple equation of state (EOS). The major limitation of this equation of state is that the gas compressibility factor, Z, is not a constant but varies from one gas to another as well as with the temperature and pressure of the gas under consideration.
More accurate values of real gas molar volumes may be obtained by using equations of state such as the van der Waals equation developed in 1873, the Redlich-Kwong equation developed in 1949, the Soave-Redlich-Kwong equation developed in 1972 and the Peng-Robinson equation developed in 1976.[3]
[edit] References
- ↑ 1.0 1.1 International Union of Pure and Applied chemistry (IUPAC): Quantities, Units and Symbols in Physical Chemistry 2nd Edition, 1993
- ↑ 2.0 2.1 NIST Guide to SI Item 8.6.3 in Section 8
- ↑ 3.0 3.1 Determination of gas compressibility values Information on how to determine gas compressibility factors and molar volumes.
| |
Some content on this page may previously have appeared on Citizendium. |