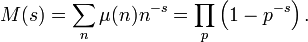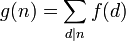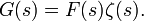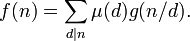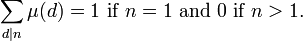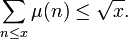Moebius function

In number theory, the Möbius function μ(n) is an arithmetic function which takes the values -1, 0 or +1 depending on the prime factorisation of its input n.

If the positive integer n has a repeated prime factor then μ(n) is defined to be zero. If n is square-free, then μ(n) = +1 if n has an even number of prime factors and -1 if n has an odd number of prime factors.

The Möbius function is multiplicative, and hence the associated formal Dirichlet series has an Euler product

Comparison with the zeta function shows that formally at least M(s) = 1 / ζ(s).

[edit] Möbius inversion formula

Let f be an arithmetic function and F(s) the corresponding formal Dirichlet series. The Dirichlet convolution

corresponds to

We therefore have

,

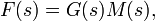giving the Möbius inversion formula

A useful special case is the formula

[edit] Mertens conjecture

The Mertens conjecture is that the summatory function

The truth of the Mertens conjecture would imply the Riemann hypothesis. However, computations by Andrew Odlyzko have shown that the Mertens conjecture is false.

Some content on this page may previously have appeared on Citizendium.