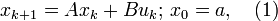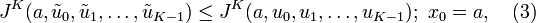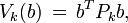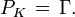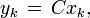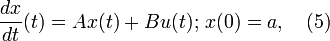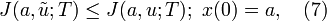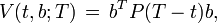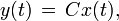Linear quadratic control
In control engineering and systems and control theory, linear quadratic control or LQ control refers to controller design for a deterministic (meaning that there are no elements of randomness involved) linear plant based on the minimization of a quadratic cost functional (a functional is a term for a real or complex valued function). The method is founded on the state space formalism and is a fundamental concept in linear systems and control theory.
There are two main versions of the method, depending on the setting of the control problem:
- Discrete time linear quadratic control
- Continuous time linear quadratic control
LQ control aims to find a control signal that minimizes a prescribed quadratic cost functional. In the so-called optimal regulator problem, this functional can be viewed as an abstraction of the "energy" of the overall control system and minimization of the functional corresponds to minimization of that energy.
Contents |
[edit] Discrete time linear quadratic control
[edit] Plant model
In discrete time, the plant (the system to be controlled) is assumed to be linear with input uk and state xk, and evolves in discrete time k=0,1,... according to the following dynamics:
where 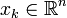 and
and 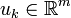 for all
for all 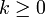 and
and 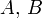 are real matrices of the corresponding sizes (i.e., for consistency, A should be of the dimension
are real matrices of the corresponding sizes (i.e., for consistency, A should be of the dimension 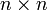 while B should be of dimension
while B should be of dimension 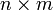 ). Here a is the initial state of the plant.
). Here a is the initial state of the plant.
[edit] Cost functional
For a finite integer K > 0, called the control horizon or horizon, a real valued cost functional J of a and the control sequence 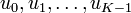 up to time K − 1 is defined as follows:
up to time K − 1 is defined as follows:
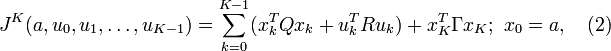
where Q,Γ are given symmetric matrices (of the corresponding sizes) satisfying 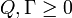 and R is a given symmetric matrix (of the corresponding size) satisfying R > 0. In this setting, control is executed for a finite time and the horizon K represents the terminal time of the control action. However, depending on some technical assumptions on the plant, it may also be possible to allow
and R is a given symmetric matrix (of the corresponding size) satisfying R > 0. In this setting, control is executed for a finite time and the horizon K represents the terminal time of the control action. However, depending on some technical assumptions on the plant, it may also be possible to allow 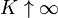 in which case one speaks of an infinite horizon.
in which case one speaks of an infinite horizon.
Note that each term on the right hand side of (2) are non-negative definite quadratic terms and may be interpreted as abstract "energy" terms (e.g., 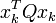 as the "energy" of xK). The term
as the "energy" of xK). The term 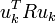 accounts for penalization of the control effort. This term is necessary because overly large control signals are not desirable in general; in practice this could mean that the resulting controller cannot be implemented. The final term
accounts for penalization of the control effort. This term is necessary because overly large control signals are not desirable in general; in practice this could mean that the resulting controller cannot be implemented. The final term 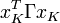 is called the terminal cost and it penalizes the energy of the plant at the final state xK .
is called the terminal cost and it penalizes the energy of the plant at the final state xK .
[edit] The LQ regulator problem in discrete time
The objective of LQ control is to solve the optimal regulator problem:
(Optimal regulator problem) For a given horizon K and initial state a, find a control sequencethat minimizes the cost functional JK, that is,
over all possible control sequences.
Thus the optimal regulator problem is a type of optimal control problem and the control sequence 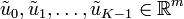 is called an optimal control sequence.
is called an optimal control sequence.
[edit] Solution of optimal regulator problem
A standard approach to solving the discrete time optimal regulator problem is to use dynamic programming. In this case, a special role is played by the so-called cost-to-go functional 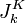 , defined as the cost from step k to step K starting at xk = b:
, defined as the cost from step k to step K starting at xk = b:
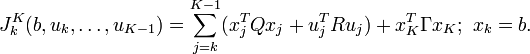
Another important notion is that of the value function at step k, Vk, defined as:
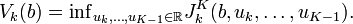
For the optimal regulator problem it can be shown that Vk is also a quadratic function (of the variable b). It is given by:
where Pk is a real non-negative definite symmetric matrix satisfying the backward recursion:
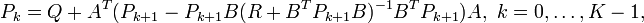
with the final condition:
Moreover, the infimum of 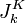 for a fixed b is attainable at the optimal sequence
for a fixed b is attainable at the optimal sequence 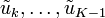 given by:
given by:
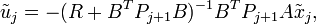
where 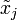 , j = k,...,K − 1, satisfies the plant dynamics with
, j = k,...,K − 1, satisfies the plant dynamics with 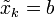 (it should be noted that in optimization problems a minimum/maximum is not guaranteed in general to be attained at some point in the domain of the functional to be minimized/maximized, this needs to be verified). It then follows that the minimum value of the cost functional (2) is simply:
(it should be noted that in optimization problems a minimum/maximum is not guaranteed in general to be attained at some point in the domain of the functional to be minimized/maximized, this needs to be verified). It then follows that the minimum value of the cost functional (2) is simply:
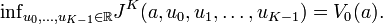
The validity of the above results depends crucially on the assumption that R > 0, this prevents the problem from becoming "singular". It also guarantees the uniqueness of the optimal sequence (i.e., there is exactly one sequence minimizing the cost functional (2)).
[edit] Variations of discrete-time LQ control
It is possible to formulate variations of the optimal regulator problem, but which can be solved with a similar technique. For example, suppose that the dynamics (1) is augmented with an output signal yk given by:
where 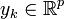 and
and 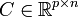 , and the cost functional JK in (2) is modified to be:
, and the cost functional JK in (2) is modified to be:
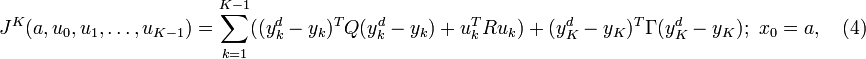
where 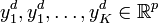 is a given sequence of desired output signals. Then a variation of the optimal regulator problem can be formulated as finding a control sequence
is a given sequence of desired output signals. Then a variation of the optimal regulator problem can be formulated as finding a control sequence 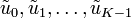 satisfying (3), but with the cost functional now being defined as in (4).
satisfying (3), but with the cost functional now being defined as in (4).
The modified problem is referred to as the output tracking LQ problem because the objective is to force the output yk of the plant at step k to be close to (i.e., to "track") the desired output 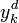 . If C is the identity matrix and
. If C is the identity matrix and 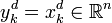 then the tracking problem can be interpreted as forcing the state of the plant to try to track the desired sequence of states
then the tracking problem can be interpreted as forcing the state of the plant to try to track the desired sequence of states 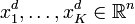 at every step.
at every step.
[edit] Continuous time linear quadratic control
An analogous formulation of LQ control as described in the above can be given in continuous time. Most of the ideas involved and techniques used in the the discrete time version can be adapted and extended to the continuous time version, but since it is necessary to deal with functions instead of sequences, the latter is more technical and additional care needs to be taken. Nonetheless, it turns out that the main results are analogous to the discrete time results.
[edit] Plant model
In the continuous time setting, the plant is again assumed to be linear with input u and state x, and evolves in 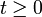 according to the following ordinary differential equation (ODE):
according to the following ordinary differential equation (ODE):
where 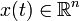 and
and 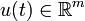 for all
for all 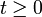 and
and 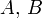 are real matrices of the corresponding sizes. As before, a is the initial state of the plant.
are real matrices of the corresponding sizes. As before, a is the initial state of the plant.
[edit] Cost functional
Let ![C([a,b];\mathbb{R}^m)](../w/images/math/e/5/f/e5f4f69352892f4a7a735b2dbafa4d2f.png) (a<b) be the set of all continuous
(a<b) be the set of all continuous 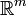 -valued functions on the interval [a,b]. For a positive number T > 0, the control horizon, a real valued cost functional J of a and the control signal
-valued functions on the interval [a,b]. For a positive number T > 0, the control horizon, a real valued cost functional J of a and the control signal ![u \in C([0,T];\mathbb{R}^m)](../w/images/math/2/6/4/264d98ff07033e41684c94ea47aeb477.png) is defined as follows:
is defined as follows:
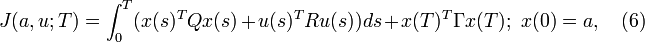
where Q,Γ are given symmetric matrices (of the corresponding sizes) satisfying 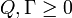 and R is a given symmetric matrix (of the corresponding size) satisfying R > 0. Control is executed for a finite time and the horizon T represents the terminal time of the control action. However, depending on some technical assumptions on the plant, it may also be possible to consider the infinite horizon case by letting
and R is a given symmetric matrix (of the corresponding size) satisfying R > 0. Control is executed for a finite time and the horizon T represents the terminal time of the control action. However, depending on some technical assumptions on the plant, it may also be possible to consider the infinite horizon case by letting 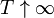 .
.
[edit] The LQ regulator problem in continuous time
The objective of continuous time LQ control is to solve the continuous time optimal regulator problem:
(Optimal regulator problem) For a given horizon T and initial state a, find a control signalthat minimizes the cost functional J, that is,
over all possible control signals.
The signal 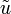 is then said to be an optimal control signal.
is then said to be an optimal control signal.
[edit] Solution of optimal regulator problem
The continuous time optimal regulator problem may also be solved by dynamic programming. In this case, a special role is played by the so-called cost-to-go functional J(t,b,u;T), defined as the cost from time t to time T starting at x(t) = b:
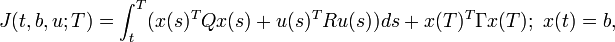
Another important notion is that of the value function at time t, V(t,b;T), defined as:
![V(t,b;T)=\mathop{\inf}_{u \in C([0,T];\mathbb{R}^m)} J(t,b,u;T).](../w/images/math/0/a/c/0ac9486e5b852a49cfd6a9ab29605349.png)
For the optimal regulator problem it can be shown that V(t,b;T) is also a quadratic function (of the variable b). It is given by:
where P(t) is a real non-negative definite symmetric matrix-valued function satisfying the so-called continuous Riccati differential equation:
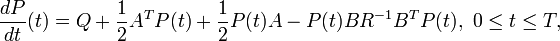
with the initial condition:
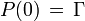 .
.
Moreover, the infimum of J(t,b,u;T) for a fixed b is attainable at the unique (due to the condition R>0) optimal control signal 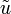 given by:
given by:
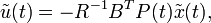
where ![\tilde x \in C([t,T];\mathbb{R}^m)](../w/images/math/f/1/f/f1f2a5dff0e398ac59508591af68ea84.png) satisfies the plant dynamics with
satisfies the plant dynamics with 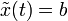 . It then follows that the minimum value of the cost functional (2) is simply:
. It then follows that the minimum value of the cost functional (2) is simply:
![\mathop{\inf}_{u \in C([0,T];\mathbb{R}^m)}J(a,u;T)=V(0,a;T).](../w/images/math/b/7/0/b70aeda4dda6c1601e9ce89524a062dc.png)
[edit] Variations of continuous time LQ control
As in the discrete time case, an output tracking variation of the optimal regulator problem can be formulated, but which can be solved with a similar technique. For example, suppose that the dynamics (5) is augmented with an output signal ![y \in C([0,T];\mathbb{R}^p)](../w/images/math/d/e/d/dede0d2e04cc7f29c9382de2f1b6984a.png) given by:
given by:
where 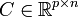 , and the cost functional J in (5) is modified to be:
, and the cost functional J in (5) is modified to be:
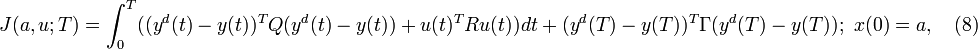
where ![y^d \in C([0,T];\mathbb{R}^p)](../w/images/math/0/0/1/0015ec7d1cff41eb71855bd5609a2579.png) is a given sequence of desired output signals. Then the output tracking variation of the optimal regulator problem can be formulated as finding a control sequence
is a given sequence of desired output signals. Then the output tracking variation of the optimal regulator problem can be formulated as finding a control sequence ![\tilde u \in C([0,T];\mathbb{R}^m)](../w/images/math/5/9/8/59802b63e94d209ffd82c4379609fde3.png) satisfying (7), but with the cost functional now being defined as in (8).
satisfying (7), but with the cost functional now being defined as in (8).
[edit] Further reading
- B.D.O. Anderson and J.B. Moore, Optimal Control: Linear Quadratic Methods, Englewood Cliffs, N.J.: Prentice-Hall, 1990.
- H. Kwakernaak and R. Sivan, Optimal Linear Control Systems, New York: Wiley Interscience, 1972.
- W. Brogan, Modern Control Theory (3 ed.), Englewood Cliffs, N.J.: Prentice Hall, 1991.
[edit] Related topics
Linear quadratic Gaussian control
| |
Some content on this page may previously have appeared on Citizendium. |