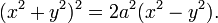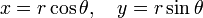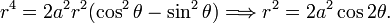Lemniscate
A lemniscate is a geometric curve in the form of the digit 8, usually drawn such that the digit is lying on its side, as the infinity symbol  . The name derives from the Greek λημνισκος (lemniskos, woolen band).
. The name derives from the Greek λημνισκος (lemniskos, woolen band).
Two forms are common.
[edit] Lemniscate of Gerono
This form is named for the French mathematician Camille Christophe Gerono (1799-1891). Its equation in Cartesian coordinates is
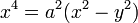 .
.
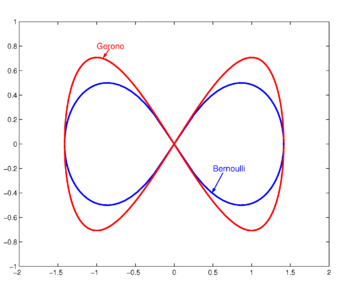
The figure shows the case a = √2
[edit] Lemniscate of Bernoulli
This form was discovered by James Bernoulli, who coined the term Curva Lemniscata, comparing the curve to a noeud de ruban (a ribbon knot) in an article in Acta Eruditorum of September 1694 (p. 336). Basically, Bernoulli's lemniscate is the locus of points that have a distance r1 to a focus F1 and a distance r2 to a focus F2, while the product r1×r2 is constant. In the figure the foci are on the x-axis at ±1. The product of the distances is constant and equal to half the distance 2a between the foci squared. For foci on the x-axis at ±a the equation is,
Expanding and simplifying gives
The latter equation gives upon substitution of
the following polar equation
Bernoulli's lemniscate belongs to the more general class of the Cassini ovals.


![r_1\,r_2 = a^2 = \left[ (x-a)^2 + y^2\right]^{\frac{1}{2}} \left[(x+a)^2 + y^2\right]^{\frac{1}{2}}.](../w/images/math/5/0/d/50df93534c3ed661bbea7c7337340e50.png)