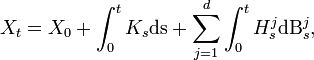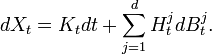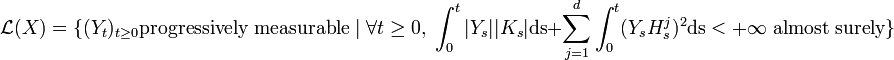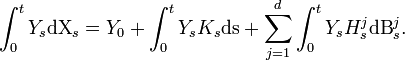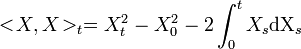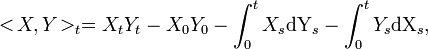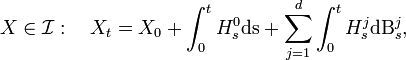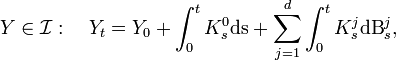Ito process
An Ito process is a type of stochastic process described by Japanese mathematician Kiyoshi Itô, which can be written as the sum of the integral of a process over time and of another process over a Brownian motion. Those processes are the base of Stochastic integration, and are therefore widely used in financial mathematics and stochastic calculus.
Contents |
[edit] Description of the Ito Processes
Let 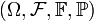 be a probability space with a filtration
be a probability space with a filtration 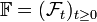 that we consider as complete (that is to say, all sets which measure is equal to zero are contained in
that we consider as complete (that is to say, all sets which measure is equal to zero are contained in 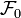 ). Let also be
). Let also be 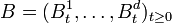 a d-dimensional
a d-dimensional 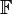 -standard Brownian motion.
Then we call "Ito process" every process
-standard Brownian motion.
Then we call "Ito process" every process 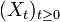 that can be written in the form
that can be written in the form
where
- X0 is
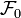 measurable,
measurable,
-
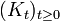 is a progressively measurable process such that
is a progressively measurable process such that 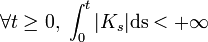 almost surely.
almost surely.
-
![(H^i_t)_{t\geq 0,\ i\in[1\dots d]}](../w/images/math/7/b/2/7b22bdc04d8a39de325bc92b53caa724.png) is progressively measurable and such as
is progressively measurable and such as ![\forall i\in [1\dots d],\; \forall t\geq 0,\; \int_0^t(H_s^i)^2\mathrm{ds}<+\infty](../w/images/math/d/b/7/db77b180b0124f070c1e9c1d1a5a4cc2.png) almost surely.
almost surely.
We denote by 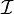 the set of all Ito processes. All Ito processes are continuous and adapted to the filtration
the set of all Ito processes. All Ito processes are continuous and adapted to the filtration 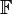 . We can also write the Ito process in the 'differential form':
. We can also write the Ito process in the 'differential form':
Using the fact that the Brownian part is a local martingal, and that all continuous local martingal with finite variations equal to zero in zero is indistinguishible from the null process, we can show that this decomposition is unique (up to indistinguishability) for each Ito process.
[edit] Stochastic Integral with respect to an Ito process
Let X be an Ito process. We can define the set of processes 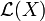 that we can integrate with respect to X:
that we can integrate with respect to X:
We can then write:
[edit] Stability of the set of Ito processes
- Stability over addition
- The sum of two Ito processes is obviously another Ito process.
- Stability over Integration
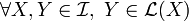 . Which means that any Ito process can be integrated with respect to any other Ito process. Moreover, the stochastic integral with respect to an Ito process is still an Ito process.
. Which means that any Ito process can be integrated with respect to any other Ito process. Moreover, the stochastic integral with respect to an Ito process is still an Ito process.
This exceptional stability is one of the reasons of the wide use of Ito processes. The other reason is the Ito formula.
[edit] Quadratic Variation of an Ito Process
Let 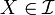 . The construction of the stochastic integral makes the usual formula for deterministic functions
. The construction of the stochastic integral makes the usual formula for deterministic functions 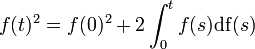 wrong for the Ito processes. We then define the quadratic variation as the process < X,X > t:
wrong for the Ito processes. We then define the quadratic variation as the process < X,X > t:
This process is adapted, continuous, equal to zero in zero, and its trajectories are almost surely increasing.
We can define similarly the covariation of two Ito processes :
which is also adapted, continuous, equal to zero in zero, and has finite variation.
We can then note the following properties of the quadratic variation:
- If X or Y has finite variation then
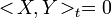
- If
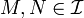 are local martingales then
are local martingales then 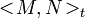 is the only adapted, continuous, vanishing at zero process of finite variation such that
is the only adapted, continuous, vanishing at zero process of finite variation such that 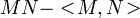 is a local martingale.
is a local martingale.
- If we have
then 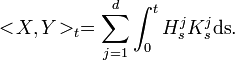
| |
Some content on this page may previously have appeared on Citizendium. |