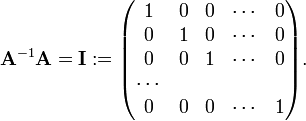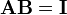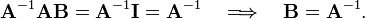Inverse matrix
From Knowino
(Redirected from Invertible matrix)
In mathematics, a square matrix A may have a left-inverse matrix A−1 defined by
If A−1 exists, the matrix A is called regular, non-singular, or invertible.
If for an invertible matrix A it holds that
then the matrix B is the right-inverse of A. Assume that A is invertible and multiply the last equation by the left-inverse
It follows that for any finite-dimensional matrix A the right-inverse matrix is equal to the left-inverse matrix, simply called the inverse of A and indicated by A−1.
A necessary and sufficient condition for the inverse A−1 to exist is the non-vanishing of the determinant: det(A) ≠ 0.
See this article for an explicit expression for the elements of A−1.