Inclusion-exclusion principle
The inclusion-exclusion principle is a theorem of combinatorics relating to the number of elements in a finite set defined as the union of a finite collection of finite sets. The general form of the theorem for n sets 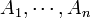 is
is 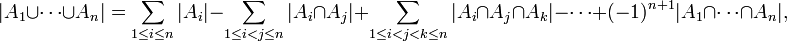 where |A| denotes the number of elements in a finite set |A| (called also the cardinality of A) . This equality may be explained intuitively by stating that if we simply take as the cardinality of the union the sum of the cardinalities of the constituent sets, then we have counted those elements that lie in more than one of those sets more than once, so we subtract the sum of the cardinalities of two-way intersections. However, now we have subtracted those elements contained in three or more sets too many times, so we have to add back the sum of the three-way intersections. This creates an overcount once again, and so we continue, alternating sign as we go, until we reach the intersection of all of the sets in the collection.
where |A| denotes the number of elements in a finite set |A| (called also the cardinality of A) . This equality may be explained intuitively by stating that if we simply take as the cardinality of the union the sum of the cardinalities of the constituent sets, then we have counted those elements that lie in more than one of those sets more than once, so we subtract the sum of the cardinalities of two-way intersections. However, now we have subtracted those elements contained in three or more sets too many times, so we have to add back the sum of the three-way intersections. This creates an overcount once again, and so we continue, alternating sign as we go, until we reach the intersection of all of the sets in the collection.
| |
Some content on this page may previously have appeared on Citizendium. |

