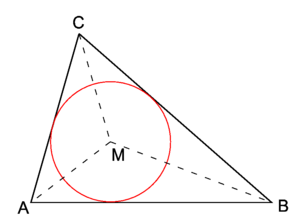
Incentre
In triangle geometry, the incentre of a triangle is the centre of the incircle, a circle which is within the triangle and tangent to its three sides. It is the common intersection of the three angle bisectors, which form a Cevian line system. The contact triangle has as vertices the three points of contact of the incircle with the three sides: it is the pedal triangle to the incentre. The inradius is the radius of the incircle: the area of the triangle is equal to the product of the inradius and the semi-perimeter. The incircle is tangent to the nine-point circle.
More generally, if a polygon has a single interior circle tangent to all its sides, this is the incircle of the polygon and the centre of the incircle is the incentre.
A circum quadrilateral is a quadrilateral with an inscribed circle. The condition for a quadrilateral to have an incircle is that the sums of the lengths of the pairs of opposite sides should be equal.
| |
Some content on this page may previously have appeared on Citizendium. |