If and only if
From Knowino
The phrase "if and only if" — in print often abbreviated to "iff" — is frequently used in mathematical language to express that two statements are (logically) equivalent, i.e., that they imply each other. Thus it has the same meaning as the phrase "necessary and sufficient".
In mathematical formulae "if and only if" is written as
"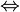 ".
".
Examples:
- Three versions of the same statement (a product is not 0 unless a factor is).
- The product of two (real) numbers is 0 if and only if at least one of the two factors equals 0.
- ab = 0 iff a = 0 or b = 0.
-
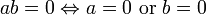
- A monotone sequence of real numbers is convergent iff it is bounded.
| |
Some content on this page may previously have appeared on Citizendium. |

