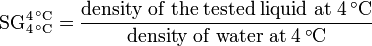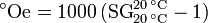Hydrometer
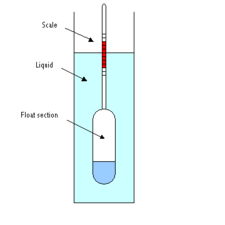
A hydrometer is an instrument typically used to measure the specific gravity (SG) (or relative density) of liquids; that is, the ratio of the density of the liquid to the density of water with both at the same temperature. It is usually made of glass and consists of a small diameter cylindrical stem and a larger diameter float section weighted with mercury or lead shot (sealed with wax) to make it float upright. The larger diameter float section is necessary to provide the displacement volume needed for the proper buoyancy of the hydrometer
The stem contains a rolled paper marked with the scale being used. There are a great many different hydrometer scales commonly used to measure liquid densities in: petroleum crude oil marketing and refining; making wine, brewing beer and making whiskey; refining sugar; producing sulfuric acid and other industrial chemicals.
In the past, hydrometers have also been referred to as gravimeters, densimeters or areometers. If the float section (see adjacent drawing) includes a built-in thermometer, the instrument is then referred to as a thermohydrometer.
[edit] Scales
The many hydrometer scales that are commonly used include:
- Specific gravity (SG)
- The specific gravity of a liquid or solid is the dimensionless ratio of the density of the liquid or solid at a given reference temperature to the density of a given reference material at a given reference temperature. The given reference material is usually water and unless the two reference temperatures are explicitly stated, they are generally taken to be 4 °C.
- The specific gravity scale is widely used in chemistry, engineering and physics as well as by geologists, mineralogists and gemologists. It is often referred to as relative density and it is the one shown in the adjacent drawing. The specific gravity scale is expressed as:
- Note 1: The specific gravity of solids can be determined by using a pycnometer rather than a hydrometer.
- Note 2: Hydrometers are not used to determine the specific gravity of gases and this article does not include any discussion of the specific gravity of gases.
- API gravity
- This scale was developed by the American Petroleum Institute (API) in 1921 for use in the petroleum industry and it is now universally used by the petroleum industry worldwide. It is expressed as:[1]
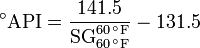 and
and 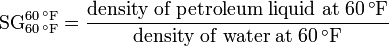
- Note: 60 °F is equivalent to 15.56 °C.
- Baumé gravity
- These two scales, one for liquids lighter than water and one for liquids heavier than water, were developed by the French chemist Antoine Baumé in 1768. It is widely used in industrial chemistry, pharmacology, sugar refining and other industries. The two scales are expressed below as:[2][3]
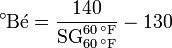 for liquids lighter than water and
for liquids lighter than water and 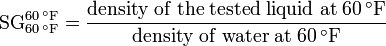
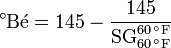 for liquids heavier than water and
for liquids heavier than water and 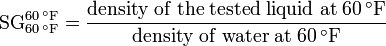
- Note: Many literature sources present the above equations with the specific gravity reference temperatures being 20°C, which ignores the small difference between specific gravities at 60 °F and 20 °C.[4]
- Brix gravity
- This scale was developed in the 1854 by Adolf Ferdinand Wenceslaus Brix, a German or Austrian engineer and mathematician. It is widely used in beer brewing, wineries, sugar refining and fruit juice industry. It is expressed as:[5][6]
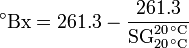 and
and 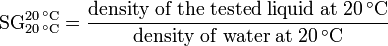
- Oechsle gravity
- This scale was developed in the 1830's by Christian Ferdinand Oechsle, a German pharmacist and goldsmith. It is used in Germany, Austria and Switzerland in wineries and beer brewing. It is expressed as:[5]
- Plato gravity
- This scale was developed in 1918 by Dr. Fritz Plato , a German scientist. It is primarily used in the beer brewing industry and it is expressed as:[7]
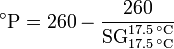 and
and 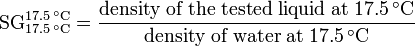
- The origin of the Plato scale lies in the Balling Scale developed in 1835 by Carl Joseph Napoleon Balling which was recalibrated by Brix in 1854 and renamed the Brix scale. In 1918, Dr. Plato then developed his scale by improving and correcting Balling's original work. Basically, the Balling, Brix and Plato scales are identical up to the fifth and sixth decimal place.[8]
- Twaddell gravity
- In the 19th century, this scale was developed in Glasgow, Scotland by William Twaddell, an instrument maker.[9] It is used in many industries and it is expressed as:[2]
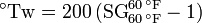 used only for liquids heavier than water
used only for liquids heavier than water
- Others
- The leather tanning industry uses a Barkometer that expresses specific gravity in Barkometer degrees.
- The dairy industry uses a Lactometer calibrated in Quevenne degrees in testing milk.
- The alcohol industry uses the Sikes, Richter, or Tralles scales on their Alcoholometers. Each of them reads the volumetric percentage of ethyl alcohol in water.
[edit] History
Knowledge of relative density or specific gravity has been with us since the days of Archimedes in 250 BC, with the observation that light objects can float while heavier ones will sink in water.[10] Hypatia (born ca. 350 and died 415 AD), a Greek scholar from Alexandria in Egypt and considered to be the first notable female mathematician, is reputed to have invented the hydrometer.[11]
Several key figures in the history of science have mentioned the hydrometer in their work, including Galileo in 1612. In the 18th and 19th centuries, industrial development in Europe spurred the need for the hydrometer. It gained fame due to public controversy over alcohol taxation since the hydrometer was used in the distillation industry to measure alcohol content and determine excise taxes in England.
A great deal more detailed history is provided in the book, edited by Holmes and Lever, about the history of instruments in chemistry from the days of the alchemists through the creation of the modern chemistry laboratory.[12]
[edit] References
- ↑ API Gravity References the publication: Ernest L. Ruh, James J. Moran and Robert D. Thompson (1959). Measurement problems in the instrument and laboratory apparatus fields. American Association for the Advancement of Science (AAAS), Page 29. AAAS Publication No. 57.
- ↑ 2.0 2.1 Perry, R.H. and Green, D.W. (1984). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw Hill, Inc., page 1-19. ISBN 0-07-049479-7.
- ↑ What is a "degree Baume'? Professor Frederick A. Senese, Chemistry Department, Frostburg State University, Maryland
- ↑ U.S. National Bureau of Standards (1913). Bureau of Standard Circular No. 41, Testing and Properties of Textile Materials. Government Printing Office, page 160. (See second paragraph below Table 32 for comment about the small difference between specific gravities at 60 °F and 20 °C.)
- ↑ 5.0 5.1 Jean L. Jacobson (2005). Introduction to Wine Laboratory Practices and Procedures, 1st Edition. Springer. 0-387-24377-1.
- ↑ Degrees Brix
- ↑ Roger B. Boulton, Vernon L. Singleton, Linda F. Bisson and Ralph E. Kunkee (1996). Principles and Practices of Winemaking, 1st Edition. Springer. ISBN 0-8342-1270-6.
- ↑ Peter Hull (2010). Glucose Syrups: Technology and Applications, 1st Edition. Wiley-Blackwell. ISBN 1-4051-7556-7. Chapter 1 is available online at Chapter 1, History of Glucose Syrups]
- ↑ Hydrometers From the website of the National Museums of Scotland.
- ↑ T. L. Heath (1897). The Works of Archimedes. Cambridge University Press, page 253. Full text available at www.archive.org
- ↑ Mothers of Invention Ethlie Ann Vare and Greg Ptacek, 1988, pp. 24-26.
- ↑ Frederick L. Holmes and Trevor H. Levere (Editors) (2002). Instruments and Experimentation in the History of Chemistry, 1st Edition, 2nd Printing. The MIT Press. ISBN 0-262-08282-9.
| |
Some content on this page may previously have appeared on Citizendium. |