Hund's rules
In atomic spectroscopy, Hund's rules predict the order of atomic energy levels with quantum numbers L (orbital), S (spin) and J (orbital plus spin). The rules are called after Friedrich Hund who formulated them in 1925.[1]
Contents |
[edit] LS coupling
A group of atomic energy levels, obtained by Russell-Saunders coupling, is concisely indicated by a term symbol. As discussed in the article Russell-Saunders coupling, closed shells and closed subshells have L = S = 0 and hence can be ignored in the coupling. A term (also known as multiplet) is a set of simultaneous eigenfunctions of L2 (total orbital angular momentum squared) and S2 (total spin angular momentum squared) with given quantum numbers L and S, respectively. That is, the respective eigenvalues are L(L+1)ℏ2 and S(S+1)ℏ2.
If there is no spin-orbit coupling, the functions of one term (fixed L and S) are (2L+1)×(2S+1)-fold degenerate (have the same energy). If there is weak spin-orbit coupling it is useful to diagonalize the matrix of the corresponding spin-orbit operator within the L-S basis [consisting of the (2L+1)×(2S+1) functions of the term] in the spirit of first-order perturbation theory. This lifts partially the degeneracy and introduces the new conserved quantum number J, with |L-S| ≤ J ≤ L+S, that labels a (2J+1)-fold degenerate energy level.
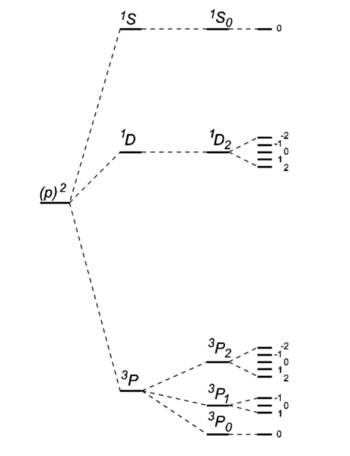
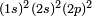 . Drawing is not on scale. On the left the energy without any two-particle interaction. Then three-fold energy splitting after switching on electrostatic electron-electron interaction (L and S good quantum numbers). Then splittings after switching on first-order spin-orbit coupling (J good quantum number). Finally on the right Zeeman splittings in an external magnetic field.
. Drawing is not on scale. On the left the energy without any two-particle interaction. Then three-fold energy splitting after switching on electrostatic electron-electron interaction (L and S good quantum numbers). Then splittings after switching on first-order spin-orbit coupling (J good quantum number). Finally on the right Zeeman splittings in an external magnetic field.[edit] Formulation of the rules
Hund's rules are:[2]
- Of the Russell-Saunders states arising from a given electron configuration those with the largest spin quantum number S lie lowest, those with the next largest next, and so on; in other words, the states with largest spin multiplicity are the most stable.
- Of the group of terms with a given value of S, that with the largest value of L lies lowest.
- Of the states with given values of S and L in an electronic configuration consisting of less than half the electrons in a closed subshell, the state with the smallest value of J is usually the most stable, and for a configuration consisting of more than half the electrons in a closed subshell the state with largest J is the most stable.
The levels of the second sort, largest J most stable, can be seen as arising from holes in a closed subshell.
[edit] Examples
- The ground state carbon atom, (1s)2(2s)2(2p)2, gives by Russell-Saunders coupling a set of energy levels labeled by term symbols. Hund's rules predict the following order of the energies:
- 3P0 < 3P1 < 3P2 < 1D2 < 1S0.
- The ground state oxygen atom, (1s)2(2s)2(2p)4, (a two-hole state) gives by Russell-Saunders coupling a set of energy levels labeled by term symbols. Hund's rules predict the following order of the energies:
- 3P2 < 3P1 < 3P0 < 1D2 < 1S0.
[edit] References
- ↑ F. Hund, Zur Deutung verwickelter Spektren, insbesondere der Elemente Scandium bis Nickel. [On the interpretation of complicated spectra, in particular the elements scandium through nickel]. Zeitschrift für Physik, vol. 33, pp. 345-371 (1925).
- ↑ L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 3rd edition (1960)

