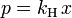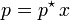Henry's law
Contents |
Henry's law is one of the gas laws, formulated by the British chemist, William Henry, in 1803. It states that:
- At a constant temperature, the amount of a given gas dissolved in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid.
[edit] Formula and Henry constant
A formula for Henry's law is:
where:
 is approximately 2.7182818, the base of the natural logarithm (also called Euler's number)
is approximately 2.7182818, the base of the natural logarithm (also called Euler's number)
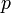 is the partial pressure of the solute above the solution
is the partial pressure of the solute above the solution
 is the concentration of the solute in the solution (in one of its many units)
is the concentration of the solute in the solution (in one of its many units)
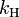 is the Henry's law constant, which has units such as L·atm/mol, atm/mole fraction or Pa·m3/mol.
is the Henry's law constant, which has units such as L·atm/mol, atm/mole fraction or Pa·m3/mol.
Taking the natural logarithm of the formula, gives us the more commonly used formula:[1][2][3][4]
Some values for 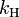 include:
include:
- oxygen (O2) : 769.2 L·atm/mol
- carbon dioxide (CO2) : 29.4 L·atm/mol
- hydrogen (H2) : 1282.1 L·atm/mol
when these gases are dissolved in water at 298 kelvins.
As shown in Table 1 below, there are other forms of Henry's law each of which defines the constant 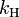 differently and requires different dimensional units.[5] The form of the equation presented above is consistent with the example numerical values presented for oxygen, carbon dioxide and hydrogen and with their corresponding dimensional units.
differently and requires different dimensional units.[5] The form of the equation presented above is consistent with the example numerical values presented for oxygen, carbon dioxide and hydrogen and with their corresponding dimensional units.
Note that for the above values, the unit of concentration, c, was chosen to be molarity (i.e., mol/L). Hence the dimensional units: L is liters of solution, atm is the partial pressure of the gaseous solute above the solution (in atmospheres of absolute pressure), and mol is the moles of the gaseous solute in the solution. Also note that the Henry's law constant, kH, varies with the solvent and the temperature.
[edit] Forms of Henry's law
There are various forms Henry's law which are discussed in the technical literature.[5][6][7]
| equation: | 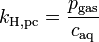 |
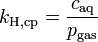 |
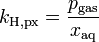 |
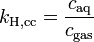
|
|---|---|---|---|---|
| dimension: | ![\left[\frac{\rm L_{\rm{soln}} \cdot \rm{atm}}{\rm{mol}_{gas}}\right]](../w/images/math/b/b/7/bb7495e7e163fed3f5a48f70d0e5a23b.png) |
![\left[\frac{\rm{mol}_{\rm{gas}}}{\rm{L}_{\rm{soln}} \cdot \rm{atm}}\right]](../w/images/math/3/a/5/3a5c8ed6891952f5a82831e28763866a.png) |
![\left[\frac{\rm{atm} \cdot \rm{mol}_{\rm{soln}}} {\rm{mol}_{\rm{gas}}}\right]](../w/images/math/f/e/1/fe17bc241ce14e797a306138da8d99d9.png) |
dimensionless |
| O2 | 769.23 | 1.3 E-3 | 4.259 E4 | 3.180 E-2 |
| H2 | 1282.05 | 7.8 E-4 | 7.099 E4 | 1.907 E-2 |
| CO2 | 29.41 | 3.4 E-2 | 0.163 E4 | 0.8317 |
| N2 | 1639.34 | 6.1 E-4 | 9.077 E4 | 1.492 E-2 |
| He | 2702.7 | 3.7 E-4 | 14.97 E4 | 9.051 E-3 |
| Ne | 2222.22 | 4.5 E-4 | 12.30 E4 | 1.101 E-2 |
| Ar | 714.28 | 1.4 E-3 | 3.955 E4 | 3.425 E-2 |
| CO | 1052.63 | 9.5 E-4 | 5.828 E4 | 2.324 E-2 |
where:
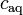 = moles of gas per liter of solution
= moles of gas per liter of solution
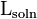 = liters of solution
= liters of solution
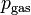 = partial pressure of gas above the solution, in atmospheres of absolute pressure
= partial pressure of gas above the solution, in atmospheres of absolute pressure
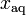 = mole fraction of gas in solution = moles of gas per mole of solution ≈ moles of gas per mole of water
= mole fraction of gas in solution = moles of gas per mole of solution ≈ moles of gas per mole of water
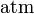 = atmospheres of absolute pressure
= atmospheres of absolute pressure
As can be seen by comparing the equations in the above table, the Henry's law constant kH,pc is simply the inverse of the constant kH,cp. Since all kH may be referred to as the Henry's Law constant, readers of the technical literature must be quite careful to note which version of the Henry's law equation is being used.[5]
It should also be noted the Henry's law is a limiting law that only applies for dilute solutions. The range of concentrations in which it applies becomes narrower the more the system diverges from ideal behavior. Roughly speaking, that is the more chemically different the solute is from the solvent.
It also only applies for solutions where the solvent does not react chemically with the gas being dissolved. A common example of a gas that does react with the solvent is carbon dioxide, which rapidly forms hydrated carbon dioxide and then carbonic acid (H2CO3) with water.
[edit] Temperature dependence of Henry's law constant
When the temperature of a system changes, the Henry's law constant will also change.[5][8] This is why some people prefer to name it Henry coefficient. There are multiple equations assessing the effect of temperature on the constant. This form of the van 't Hoff equation is one example:[7]
| where: | |
| T | = any given temperature, in kelvins |
| TΘ | = the standard state temperature of 298 K |
| kH,cp | = the solubility form of Henry's law constant at the given temperature (in the units shown in Table 1) [9] |
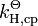
|
= the solubility form of Henry's law constant at TΘ |
| exp | = the exponential function |
| C | = a constant with dimension of kelvins |
The above equation is an approximation only and should be used only when no better experimentally derived formula for a given gas exists.
The following table lists some values for constant C in the equation above:
| Gas | O2 | H2 | CO2 | N2 | He | Ne | Ar | CO |
| C | 1700 | 500 | 2400 | 1300 | 230 | 490 | 1300 | 1300 |
Because solubility of gases decreases with increasing temperature, the partial pressure a given gas concentration has in liquid must increase. While heating water (saturated with nitrogen) from 25 °C to 95 °C the solubility will decrease to about 43% of its initial value. Partial pressure of CO2 in seawater doubles with every 16 K increase in temperature.[10]
The constant C may be regarded as:
- where:
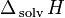
is the enthalpy of solution R is the universal gas constant
[edit] Henry's law in geophysics
In geophysics a version of Henry's law applies to the solubility of a noble gas in contact with silicate melt. One equation used is
where: ρ = the densities of the solute gas in the melt and in the gas phases β = 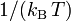 , an inverse temperature scale
, an inverse temperature scale
kB = the Boltzmann constant μE = the excess chemical potentials of the solute gas in the melt and in the gas phases
[edit] Raoult's law compared to Henry's Law
In the mathematical expressions of the two laws, both state that the partial pressure of a component in a solution is proportional to the concentration of that component in the solution. Using mole fractions, x, as the expression of concentration, Henry's law can be written as:
This can be compared with Raoult's law:
where 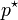 is the vapor pressure of the pure component.
is the vapor pressure of the pure component.
Thus, Raoult's law appears to be a special case of Henry's law where kH is equal to 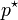 . This is true for pairs of closely related substances, such as benzene and toluene, which obey Raoult's law over the entire composition range (such mixtures are called ideal mixtures).
. This is true for pairs of closely related substances, such as benzene and toluene, which obey Raoult's law over the entire composition range (such mixtures are called ideal mixtures).
The general case is that both laws are limit laws, and they apply at opposite ends of the composition range. The vapor pressure of the component with largest concentration by far, such as the solvent for a dilute solution, is proportional to the mole fraction, and the proportionality constant is the vapor pressure of the pure substance (Raoult's law).
The vapor pressure of component with the smallest concentration by far, such as the solute in a dilute solution, is also proportional to the mole fraction, but the proportionality constant is the Henry's law constant which must be determined experimentally (Henry's law).
In mathematical terms:
- Raoult's law:
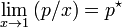
- Henry's law:
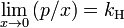
[edit] References
- ↑ http://www.udel.edu/pchem/C443/Lectures/Lecture33.pdf University of Delaware physical chemistry lecture]
- ↑ Robert G. Mortimer (2000). Physical Chemistry, Second Edition. Academic Press. ISBN 0-12-508345-9.
- ↑ Green, Don W. and Perry, Robert H. (deceased) (1984). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw-Hill. ISBN 0-07-049479-7. (See page 14-9)
- ↑ Online Introductory Chemistry: Solubility of gases in liquids
- ↑ 5.0 5.1 5.2 5.3 Francis L. Smith and Allan H. Harvey (September 2007). "Avoid Common Pitfalls When Using Henry's Law". CEP (Chemical Engineering Progress). ISSN 0360-7275.
- ↑ University of Arizona chemistry class notes
- ↑ 7.0 7.1 7.2 An extensive list of Henry's law constants, and a conversion tool
- ↑ Green, Don W. and Perry, Robert H. (deceased) (1984). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw-Hill. ISBN 0-07-049479-7. (See pages 3-101 to 3-103 for tabulated Henry's law constant values versus temperature for various gases)
- ↑ kH,cp is the same as kH, the solubility form of Henry's law constant defined by equation (1) in reference 7
- ↑ Takahashi, T. et al (2002). Global sea-air CO2 flux based on climatological surface ocean CO2 and seasonal biological and temperature effects, Deep-Sea Research (Part II, Topical Studies in Oceanography) 49, 9-10, pp. 1601-1622.
| |
Some content on this page may previously have appeared on Citizendium. |

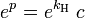

![k_{\rm H,cp} = k_{\rm H,cp}^\Theta \; \exp \left[ -C \cdot \left( \frac{1}{T}-\frac{1}{T^\Theta}\right)\right]](../w/images/math/5/7/8/578fd59789d9cbb6ff58a8190767ca89.png)
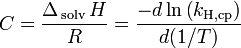
![\rho_{\rm melt}/\rho_{\rm gas} = \exp\left[-\beta(\mu^{\rm E}_{\rm melt} - \mu^{\rm E}_{\rm gas})\right]\,](../w/images/math/7/2/a/72a5e2cbb86c14e008f0a941eb9deb17.png)