Galois theory
Galois theory is an area of mathematical study that originated with Evariste Galois around 1830, as part of an effort to understand the relationships between the roots of polynomials, in particular why there are no simple formulas for extracting the roots of the general polynomial of fifth (or higher) degree.
Contents |
[edit] Introduction
Galois expressed his theory in terms of polynomials and complex numbers, today Galois theory is usually formulated using general field theory.
Key concepts are field extensions and groups, which should be thoroughly understood before Galois theory can be properly studied.
[edit] Basic summary of Galois theory
The core idea behind Galois theory is that given a polynomial f with coefficients in a field K (typically the rational numbers), there exists
- a smallest possible field L that contains K (or a field isomorphic to K) as a subfield and also all the roots of f. This field is known as the extension of K by the roots of f, or the splitting field of f over K. It is unique up to isomorphism.
- a collection of similarly defined intermediate fields, each containing a unique subset of the roots.
- a group containing all field automorphisms in L that leave the elements in K untouched - the Galois group of the polynomial f.
Providing certain technicalities are fulfilled, the structure of this group contains information about the nature of the roots, and whether the equation f = 0 has solutions expressible as a finite formula involving only ordinary arithmetical operations (addition, subtraction, multiplication, division and rational powers) on the coefficients.
This connection between the Galois group and collection of extension fields is known as the Galois connection.
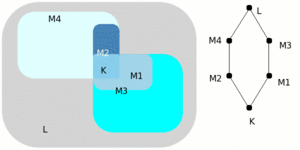
[edit] The Galois connection
Given a Galois group G we may look for all its subgroups. These subgroups again contain subgroups. This structure is naturally represented by a directed graph.
The collection of intermediate fields may also be represented by such a graph. When the Galois correspondence exists, these graphs are isomorphic.
[edit] The Galois group of a polynomial - a trivial example
As an example, let us look at the second-degree polynomial x2 − 5, with the coefficients {-5,0,1} viewed as elements of Q.
This polynomial has no roots in Q. However, from the Fundamental Theorem of Algebra we know that it has exacly two roots in C, and can be written as the product of two first-degree polynomials there - i.e. 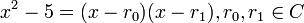 . From direct inspection of the polynomial we also realize that r0 = − r1.
. From direct inspection of the polynomial we also realize that r0 = − r1.
Using ordinary algebra and the identity 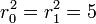 , it is quite easy to show that L =
, it is quite easy to show that L = 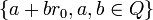 is the smallest subfield of C that contains Q and both roots.
is the smallest subfield of C that contains Q and both roots.
There are exactly 2 automorphisms of L that leave every element of Q alone: the do-nothing automorphism 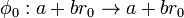 and the map
and the map 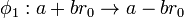 .
.
Under composition of automorphisms, these two automorphisms together form a group isomorphic to S2, the group of permutations of two objects.
The sought for Galois group is therefore S2, which has no nontrivial subgroups.
It can be shown that in this case the Galois correspondence exists, so we may conclude from the subgroup structure of S2 that there is no intermediate subfield of L containing Q and also some of the roots of the polynomial.
[edit] See also
[edit] Related topics
[edit] References
- I Stewart (1989). Galois Theory second edition. Chapman & Hall . ISBN 978-0412345500 / ISBN 0-412-34550-1.
[edit] External links
- An Introduction to Galois Theory by Andrew Baker.
| |
Some content on this page may previously have appeared on Citizendium. |