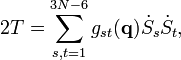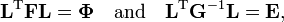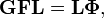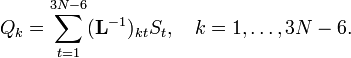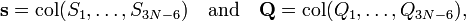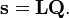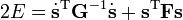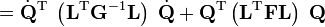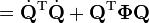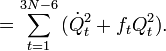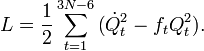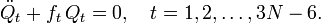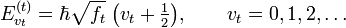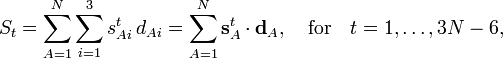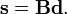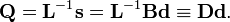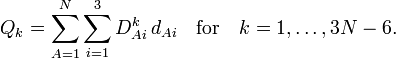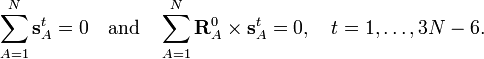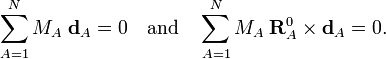GF method
In chemistry and molecular physics, the GF method, sometimes referred to as the FG method, is a classical mechanical method to obtain certain internal coordinates of a vibrating semi-rigid molecule, the so-called normal coordinates. The method was introduced by E. Bright Wilson, Jr. (1908–1992).[1]
In Wilson's GF method it is assumed that the kinetic molecular energy consists only of contributions from atomic vibrations, i.e., the overall rotational and translational kinetic energies of the molecule are neglected and the presence of electrons is ignored. Since the description of the overall rotational and translational motions of a (non-linear) molecule requires 6 coordinates and an N-atomic molecule has 3N degrees of freedom, if follows that the molecular vibrational problem has 3N−6 degrees of freedom.
In principle, the vibrations of atoms in a molecule are all coupled; roughly speaking, an N-atomic molecule can be seen as a system of 3N−6 coupled oscillators. Normal coordinates decouple these classical vibrational motions, thus making it possible to compute the harmonic vibrational displacements of the atoms as a function of time. Normal coordinates also appear in the quantum mechanical descriptions of the vibrational motions of molecules and in the Coriolis coupling between rotations and vibrations.
It follows from application of the Eckart conditions that the inverse of a matrix G gives the vibrational kinetic energy in terms of arbitrary linearized internal coordinates, while a matrix F represents the harmonic potential energy in terms of these coordinates. Solution of the GF equations gives the transformation from the linearized internal coordinates to the normal coordinates. The associated energies of the vibrations are obtained after fixing initial amplitudes (classically) or vibrational quantum numbers (quantum mechanically).
Contents |
[edit] The GF method
A non-linear molecule consisting of N atoms has 3N−6 internal degrees of freedom, because the positioning of a molecule in three-dimensional space requires three degrees of freedom and the description of its orientation requires another three degree of freedom. These six degrees of freedom must be subtracted from the 3N degrees of freedom of a system of N particles.
The atoms in a molecule are bound by a potential energy surface (PES) (also known as force field) which is a function of 3N−6 coordinates. The internal degrees of freedom q1, ..., q3N−6 describing the PES in an optimum way are often non-linear; they are for instance valence coordinates, such as bending and torsion angles and bond stretches. It is possible to write the quantum mechanical kinetic energy operator for such curvilinear coordinates, but it is hard to formulate a general theory applicable to any molecule. This is why Wilson[1] linearized the internal coordinates by assuming small displacements. The linearized version of the internal coordinate qt is denoted by St.
The PES V can be Taylor-expanded around its minimum in terms of the St. The third term (the Hessian of V) evaluated in the minimum is a force constant matrix F. In the harmonic approximation—on which the method is based—the Taylor series is ended after this quadratic term. The second term, containing first derivatives, is zero because it is evaluated in the minimum of V. The first term can be included in the zero of energy. Thus,
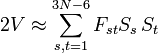 .
.
The classical vibrational kinetic energy has the form:
where gst is an element of the metric tensor of the internal (curvilinear) coordinates. The dots indicate time derivatives. Evaluation of the metric tensor g(q) in the minimum q0 of V gives the positive definite and symmetric matrix G ≡ g(q0)−1.
It is assumed that both F and G can be determined. The (inverse of the) kinetic energy matrix G is usually obtained by analytic methods and the force constant matrix F by fitting to experimental infrared data and/or quantum chemical calculations. Knowing the matrices, one can solve the following two problems simultaneously
where 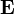 is the identity matrix.
This can be done because the two equations are equivalent to the generalized eigenvalue problem
is the identity matrix.
This can be done because the two equations are equivalent to the generalized eigenvalue problem
where 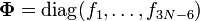 .
In numerical mathematics several algorithms are known to solve generalized eigenvalue problems. The solution yields the matrix L and the diagonal matrix Φ that has the vibrational force constants on the diagonal.
The matrix L−1 contains the normal coordinates Qk in its rows:
.
In numerical mathematics several algorithms are known to solve generalized eigenvalue problems. The solution yields the matrix L and the diagonal matrix Φ that has the vibrational force constants on the diagonal.
The matrix L−1 contains the normal coordinates Qk in its rows:
Because of the form of the generalized eigenvalue problem, the method is called the GF method, often with the name of its originator attached to it: Wilson's GF method. It is of interest to point out that by matrix transposition of both sides of the equation and by use of the fact that both G and F are symmetric, (as is a diagonal matrix), one can recast this equation into a very similar one for FG . This is why the method is also referred to as Wilson's FG method.
We introduce the vectors
which satisfy the relation
Upon use of the results of the generalized eigenvalue equation the classical (i.e., non-quantum mechanical) energy E = T + V of the molecule becomes in the harmonic approximation,
Solution of the GF equations yields Qt and ft. Classically, the time dependence of the harmonic oscillators is given by sine-type functions, so that the time derivatives of the Qt's are simple cosine-type functions. Hence E is given up to a choice of 3N−6 initial vibrational amplitudes At.
The Lagrangian L = T − V is
The corresponding Lagrange equations are identical to a set of harmonic oscillator (Newton) equations
In summary, by solving the GF equations the coupled equations have been uncoupled into a set of 3N−6 one-dimensional harmonic oscillator equations. These ordinary second-order differential equations are easily solved yielding the Qt's as sine-type functions of time, see the article on harmonic oscillators. Classically, one must further specify amplitudes At as initial conditions in order to fix the 3N−6 vibrational energies completely. Since the classical vibrational energy of a single mode is given by ½ ft (At)² this means that one must fix the initial amount of energy that is contained in each mode.
The uncoupled harmonic oscillator equations can be solved quantum mechanically as well. The energies are (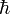 is Planck's reduced constant)
is Planck's reduced constant)
which implies that quantum mechanically 3N−6 vibrational quantum numbers vt must specified in order to fix the vibrational energy of the molecule completely. Hence, also quantum mechanically one must establish how much initial energy is present in each mode. Of course, quantum mechanics can account for excitations of vibrational modes by absorption of (infrared) photons. Classical mechanics cannot treat these quantized excitations.
[edit] Normal coordinates in terms of Cartesian displacement coordinates
Often the normal coordinates are expressed as linear combinations of Cartesian displacement coordinates.
Let RA be the position vector of nucleus A and RA0
the corresponding equilibrium position. Then
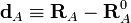 is by definition the Cartesian displacement coordinate of nucleus A.
Wilson's linearizing of the internal curvilinear coordinates qt expresses the coordinate St in terms of the displacement coordinates
is by definition the Cartesian displacement coordinate of nucleus A.
Wilson's linearizing of the internal curvilinear coordinates qt expresses the coordinate St in terms of the displacement coordinates
where sAt is known as a Wilson s-vector.
If we put the 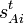 into a 3N-6 x 3N matrix B, this equation becomes in matrix language
into a 3N-6 x 3N matrix B, this equation becomes in matrix language
The actual form of the matrix elements of B can be fairly complicated.
Especially for a torsion angle, which involves 4 atoms, it requires tedious vector algebra to derive the corresponding values of the 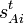 . See for more details on this method, known as
the Wilson s-vector method, the book by Wilson et al., or molecular vibration. Now,
. See for more details on this method, known as
the Wilson s-vector method, the book by Wilson et al., or molecular vibration. Now,
In summation language:
Here D is a 3N-6 x 3N matrix which is given by (i) the linearization of the internal coordinates q (an algebraic process) and (ii) solution of Wilson's GF equations (a numeric process).
[edit] Relation with Eckart conditions
From the invariance of the internal coordinates St under overall rotation and translation of the molecule, follows the same for the linearized coordinates stA. It can be shown that this implies that the following 6 conditions are satisfied by the internal coordinates,
These conditions follow from the Eckart conditions that hold for the displacement vectors,
See this article for more details.
[edit] References
Cited reference
- ↑ 1.0 1.1 E. B. Wilson, Jr. Some Mathematical Methods for the Study of Molecular Vibrations, J. Chem. Phys. vol. 9, pp. 76-84 (1941)
Further references
- E. B. Wilson, J. C. Decius, and P. C. Cross, Molecular Vibrations, McGraw-Hill, New York, 1955 (Reprinted by Dover 1980).
- D. Papoušek and M. R. Aliev, Molecular Vibrational-Rotational Spectra Elsevier, Amsterdam, 1982.
- S. Califano, Vibrational States, Wiley, London, 1976.