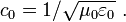Free space (electromagnetism)
Free space usually refers to a perfect vacuum, devoid of all particles. The term is most often used in classical electromagnetism where it refers to a reference state sometimes called classical vacuum,[1] and in quantum physics where it refers to the ground state of the electromagnetic field, which is subject to fluctuations about a dormant zero average-field condition.[2] The classical case of vanishing fields implies all fields are source-attributed, while in the quantum case field moments can arise without sources by virtual photon creation and destruction.[3] The description of free space varies somewhat among authors, with some authors requiring only the absence of substances with electrical properties,[4] or of charged matter (ions and electrons, for example).[5]
Contents |
[edit] Classical case
In classical physics, free space is a concept of electromagnetic theory, corresponding to a theoretically perfect vacuum and sometimes referred to as the vacuum of free space, or as classical vacuum, and is appropriately viewed as a reference medium.[1] In the classical case, free space is characterized by the electrical permittivity ε0 and the magnetic permeability μ0.[6] The exact value of ε0 is provided by NIST as the electric constant [7] and the defined value of μ0 as the magnetic constant:[8]
where the approximation is not a physical uncertainty (such as a measurement error) but a result of the inability to express these irrational numbers with a finite number of digits.
One consequence of these electromagnetic properties coupled with Maxwell's equations is that the speed of light in free space is related to ε0 and μ0 via the relation:[9]
Using the defined valued for the speed of light provided by NIST as:[10]
- c0 = 299 792 458 m s −1,
and the already mentioned defined value for μ0, this relationship leads to the exact value given above for ε0.
Another consequence of these electromagnetic properties is that the ratio of electric to magnetic field strengths in an electromagnetic wave propagating in free space is an exact value provided by NIST as the characteristic impedance of vacuum:[11]
-
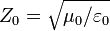
- = 376.730 313 461... Ω.
-
It also can be noted that the electrical permittivity ε0 and the magnetic permeability μ0 do not depend upon direction, field strength, polarization, or frequency. Consequently, free space is isotropic, linear, non-dichroic, and dispersion free. Linearity, in particular, implies that the fields and/or potentials due to an assembly of charges is simply the addition of the fields/potentials due to each charge separately (that is, the principle of superposition applies).[12]
[edit] Quantum case
For a discussion of the quantum case, see Vacuum (quantum electrodynamic).
[edit] Attainability
A perfect vacuum is itself only realizable in principle.[13][14] It is an idealization, like absolute zero for temperature, that can be approached, but never actually realized:[13]
“One reason [a vacuum is not empty] is that the walls of a vacuum chamber emit light in the form of black-body radiation...If this soup of photons is in thermodynamic equilibrium with the walls, it can be said to have a particular temperature, as well as a pressure. Another reason that perfect vacuum is impossible is the Heisenberg uncertainty principle which states that no particles can ever have an exact position...More fundamentally, quantum mechanics predicts ... a correction to the energy called the zero-point energy [that] consists of energies of virtual particles that have a brief existence. This is called vacuum fluctuation.”
|
And classical vacuum is one step further removed from attainability because its permittivity ε0 and permeability μ0 do not allow for quantum fluctuations. Nonetheless, outer space and good terrestrial vacuums are modeled adequately by classical vacuum for many purposes.
[edit] References
- ↑ 1.0 1.1 Werner S. Weiglhofer and Akhlesh Lakhtakia (2003). “§4.1: The classical vacuum as reference medium”, Introduction to complex mediums for optics and electromagnetics. SPIE Press. ISBN 0819449474.
- ↑ Ramamurti Shankar (1994). Principles of quantum mechanics, 2nd ed.. Springer, p. 507. ISBN 0306447908.
- ↑ Werner Vogel, Dirk-Gunnar Welsch (2006). Quantum optics, 3rd ed.. Wiley-VCH, p. 337. ISBN 3527405070.
- ↑ RK Pathria (2003). The Theory of Relativity, Reprint of Hindustan 1974 2nd ed.. Courier Dover Publications, p. 119. ISBN 0486428192.
- ↑ (1992) Christopher G. Morris, editor: Academic Press dictionary of science and technology. Academic, p. 880. ISBN 0122004000.
- ↑ Akhlesh Lakhtakia, R. Messier (2005). “§6.2: Constitutive relations”, Sculptured thin films: nanoengineered morphology and optics. SPIE Press, p. 105. ISBN 0819456063.
- ↑ CODATA. Electric constant. 2006 CODATA recommended values. NIST. Retrieved on 2010-11-28.
- ↑ CODATA. Magnetic constant. 2006 CODATA recommended values. NIST. Retrieved on 2010-11-28.
- ↑ Albrecht Unsöld, B. Baschek (2001). “§4.1: Electromagnetic radiation, Equation 4.3”, The new cosmos: an introduction to astronomy and astrophysics, 5th ed.. Springer, p. 101. ISBN 3540678778.
- ↑ CODATA. Speed of light in vacuum. 2006 CODATA recommended values. NIST. Retrieved on 2010-11-28. A defined value for the speed of light is a consequence of adoption of time of transit as the measure of length, so lengths are measured in seconds. See metre.
- ↑ CODATA. Characteristic impedance of vacuum Z0. 2006 CODATA recommended values. NIST. Retrieved on 2010-11-28.
- ↑ A. Pramanik (2004). “§1.3 The principle of superposition”, Electro-Magnetism: Theory and Applications. PHI Learning Pvt. Ltd, pp. 37-38. ISBN 8120319575.
- ↑ 13.0 13.1 Luciano Boi (2009). “Creating the physical world ex nihilo? On the quantum vacuum and its fluctuations”, Ernesto Carafoli, Gian Antonio Danieli, Giuseppe O. Longo, editors: The Two Cultures: Shared Problems. Springer, p. 55. ISBN 8847008689.
- ↑ PAM Dirac (2001). Jong-Ping Hsu, Yuanzhong Zhang, editors: Lorentz and Poincaré invariance: 100 years of relativity. World Scientific, p. 440. ISBN 9810247214.
| |
Some content on this page may previously have appeared on Citizendium. |