Dissociation constant
In biochemistry, chemistry and physics, the binding interaction of two molecules that bind with each other, for example a protein and a DNA duplex, is often quantified in terms of a dissociation constant, abbreviated as Kd, which is the inverse of the association constant, or Ka. The strength of the binding interaction is inversely proportional to Kd. Extremely tight-binding molecules such as antibodies and the their target exhibit Kd values in the picomolar range (10−12), while many drugs bind to their targets with Kd values in the nanomolar (10−9) to micromolar (10−6) range. Given the Kd of an interaction, and the initial concentrations of the interacting molecules, the amount of complex can be calculated.
[edit] Biomolecular Definition
Given two molecules, A and B, with initial molar concentrations [A]0 and [B]0, that form a reversible binding complex AB, having a certain dissociation constant Kd, that is,
The Kd, by definition, is
Using the facts that [A] = [A]0 − [AB] and [B] = [B]0 − [AB] gives
expanding the top terms yields
Multiplying both sides by [AB] and rearranging gives a quadratic equation:
whose solution is:
Given the physical limitation that [AB] cannot be greater than either [A]0 or [B]0 eliminates the solution in which the square root term is added to the first term.
[edit] Implications
An inspection of the resulting solution shown above illustrates that in order to have an appreciable amount of bound material, the interacting molecules must be present at concentrations of 1/100 to 100 times the dissociation constant, as demonstrated in the table below, in which the concentrations of A and B are expressed in units of Kd.
| [A]/Kd | [B]/Kd | %B bound ([AB]/[B])*100 |
|---|---|---|
| 0.001 | 0.001 | 0% |
| 0.01 | 0.01 | 1% |
| 0.1 | 0.1 | 8% |
| 1.0 | 1.0 | 38% |
| 10 | 10 | 73% |
| 100 | 100 | 90% |
| 1000 | 1000 | 97% |
| |
Some content on this page may previously have appeared on Citizendium. |


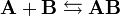
![\mathbf{K_d} = \frac{\mathbf{[A]}\times\mathbf{[B]}}{\mathbf{[AB]}}](../w/images/math/4/7/4/47410195285583fd7759c5feae0486d7.png)
![\mathbf{K_d} = \frac{(\mathbf{[A]_0} - \mathbf{[AB]})\times(\mathbf{[B]_0} - \mathbf{[AB]})}{\mathbf{[AB]}}](../w/images/math/b/a/a/baa698ec8d5c0cb79e23d1b2d3579be3.png)
![\mathbf{K_d} = \frac{\mathbf{[A]_0} \times \mathbf{[B]_0} - \mathbf{[A]_0} \times \mathbf{[AB]} - \mathbf{[B]_0} \times \mathbf{[AB]} + \mathbf{[AB]} \times \mathbf{[AB]}}{\mathbf{[AB]}}](../w/images/math/e/e/2/ee25c520460d76ddfefde8d44f8c91d4.png)
![\mathbf{[AB]^2} - \left(\mathbf{[A]_0} + \mathbf{[B]_0} + \mathbf{K_d}\right) \times \mathbf{[AB]} + \left(\mathbf{[A]_0} \times \mathbf{[B]_0}\right) = \mathbf{0}](../w/images/math/7/d/9/7d9ae03e3f8805a58bdb0ae6d2defba7.png)
![\mathbf{[AB]} = \frac{(\mathbf{[A]_0} + \mathbf{[B]_0} + \mathbf{K_d}) \pm \sqrt{(\mathbf{[A]_0} + \mathbf{[B]_0} + \mathbf{K_d)^2} - \mathbf{4} \mathbf{[A]_0} \mathbf{[B]_0}}}{\mathbf{2}}](../w/images/math/8/3/f/83f0fad58e7ea5b5401696db0dcf6ffc.png)