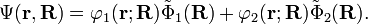Diabatic transformation
In quantum chemistry, the solution of a set of coupled nuclear motion Schrödinger equations can be facilitated by a diabatic transformation. Such a set of coupled equations, describing the motions of nuclei (in a molecule often nuclear vibrations), arises when the Born-Oppenheimer approximation breaks down. The term diabatic was coined in the 1960s. Around that time shortcomings of the Born-Oppenheimer approximation (also known as the adiabatic approximation) became apparent and improvements of the adiabatic approximation were put forward under the name diabatic approximation. Linguistically, the term "diabatic" is unfortunate because there is no connection whatsoever to the Greek word diabasis (going through).
[edit] Break-down of Born-Oppenheimer approximation
- See the article Born-Oppenheimer approximation for more details.
The Born-Oppenheimer approximation, mainly designed for quantum mechanical computation of molecular properties, but also applicable to the solid state and molecular scattering, consists of two steps. In the first step the nuclei of the system are fixed in a certain constellation and the nuclear kinetic energies are dropped from the problem, i.e., the nuclei are assumed to be at rest. One or more electronic Schrödinger equations are solved yielding the corresponding (usually the lowest or the lowest few) electronic energies. Changing sufficiently often the nuclear constellation of the system under study and solving the electronic Schrödinger equations over and over again, gives the electronic energies as functions of the nuclear coordinates. These functions are known as adiabatic potential energy surfaces.
The second step of the original Born-Oppenheimer approximation sets the nuclei in motion. This step consists of the solution of single (uncoupled) Schrödinger equations for the nuclei. In each of these equations the nuclear kinetic energy is reintroduced and a single adiabatic potential obtained from the first step serves as potential. This simple approximation breaks down when the potential energy surfaces approach—or maybe even intersect—each other. In that case the nuclear motion equations that are coupled formally by nuclear kinetic energy terms, may no longer be taken to be uncoupled, that is, the off-diagonal, nuclear kinetic energy, coupling terms may no longer assumed to be negligibly small. The equations cannot be solved one by one, but the coupled set must be tackled in its entirety.
In summary, when the Born-Oppenheimer approximation breaks down because of the presence of close lying potential energy surfaces, the solution of the nuclear motion problem requires the solution of a coupled set of Schrödinger equations. A diabatic transformation of this set of equations has the purpose of making the equations easier to solve. It is a linear (usually unitary) transformation that minimizes (preferably makes zero) the off-diagonal nuclear kinetic energy terms. The adiabatic potential energy surfaces are combined linearly to a set of diabatic potentials, which include off-diagonal terms—a diabatic transformation is a transformation from an adiabatic representation to a diabatic representation. In the latter representation the nuclear kinetic energy operator is (almost) diagonal, but the equations are still coupled, this time by off-diagonal diabatic potential terms. The advantage of the newly introduced off-diagonal potential terms is that they are significantly easier to estimate numerically than the off-diagonal nuclear kinetic energy terms that appeared before transformation.
The diabatic potential energy surfaces are smooth, so that low order Taylor series expansions of the surfaces may be applied and the expansions do not introduce a great loss of the complexity of the original system.
Unfortunately, in general a strictly diabatic transformation does not exist, it is not possible to transform the off-diagonal nuclear kinetic energy rigorously to zero. Hence, diabatic potentials generated from mixing linearly multiple electronic energy surfaces are generally not exact. These surfaces are sometimes called pseudo-diabatic potentials, but generally the term is not used unless it is necessary to highlight this subtlety; usually diabatic potentials are synonymous with pseudo-diabatic potentials.
[edit] Mathematical formulation
In order to introduce mathematically the diabatic transformation we assume now, for the sake of argument, that only two adiabatic potential energy surfaces (PES), E1 and E2, approach each other and that all other surfaces are well separated (do not come close to E1 or E2); the argument can be generalized to more surfaces.
Let the collection of electronic coordinates be indicated by r, while R indicates dependence on nuclear coordinates. Thus, we assume E1(R) ≈ E2(R) with corresponding orthonormal electronic eigenstates χ1(r;R) and χ2(r;R). In the absence of magnetic interactions these electronic states, which depend parametrically on the nuclear coordinates, may be taken to be real-valued functions.
The nuclear kinetic energy is a sum over nuclei A with mass MA,
(Atomic units are used here and ∇Aα is the a component of the gradient operator, short-hand for a differential.) By applying the Leibniz rule for differentiation, the matrix elements of Tn are (where coordinates are suppressed for clarity reasons):
The subscript r indicates that the integration inside the braket is over electronic coordinates only. The round brackets indicate the range of differentiation.
Assume that the off-diagonal matrix elements
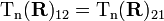 may not be neglected (in agreement with the assumption that only two surfaces approach each other, off-diagonal matrix elements with k, k′ > 2 are negligible, so that only a set of two coupled equations has to be considered). Upon making the expansion
may not be neglected (in agreement with the assumption that only two surfaces approach each other, off-diagonal matrix elements with k, k′ > 2 are negligible, so that only a set of two coupled equations has to be considered). Upon making the expansion
the two coupled nuclear Schrödinger equations take the form (see the article Born-Oppenheimer approximation)
where E is the total (electronic plus nuclear motion) energy of the molecule.
In order to remove the problematic off-diagonal kinetic energy terms, two new orthonormal states are defined by a diabatic transformation of the adiabatic states χ1(r;R) and χ2(r;R)
where γ(R) is the diabatic angle. Transformation of the matrix of nuclear momentum 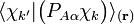 for k′, k =1,2 gives for diagonal matrix elements:
for k′, k =1,2 gives for diagonal matrix elements:
These elements are zero because 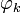 is real
and
is real
and 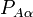 is Hermitian and pure-imaginary.
The off-diagonal elements of the momentum operator satisfy,
is Hermitian and pure-imaginary.
The off-diagonal elements of the momentum operator satisfy,
Assume that a diabatic angle γ(R) exists, such that to a good approximation the right-hand side of the last equation vanishes,
i.e., 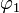 and
and 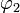 diagonalize the 2 x 2 matrix of the nuclear momentum. By the definition of Felix Smith
diagonalize the 2 x 2 matrix of the nuclear momentum. By the definition of Felix Smith 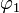 and
and 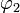 are diabatic states.[1] (Smith was the first to define this concept; earlier the term diabatic was used somewhat loosely by Lichten.[2])
are diabatic states.[1] (Smith was the first to define this concept; earlier the term diabatic was used somewhat loosely by Lichten.[2])
By a small change of notation these differential equations for γ(R) can be rewritten in the following more familiar form reminiscent of Newton's equations,
It is well-known that the differential equations have a solution (i.e., the "potential" V exists) if and only if the vector field ("force") FAα(R) is irrotational,
It can be shown that these conditions are rarely ever satisfied, so that a strictly diabatic
transformation rarely ever exists. It is common to use approximate functions 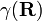 leading to pseudo diabatic states.
leading to pseudo diabatic states.
Under the assumption that the momentum operators are represented exactly by 2 x 2 matrices, which is consistent with neglect of off-diagonal elements other than the (1,2) element, and the assumption of "strict" (not pseudo) diabaticity, it can be shown that
On the basis of the diabatic states the nuclear motion problem [Eq. (1)] takes the following form
It is important to note that the off-diagonal elements (that appear only in the second term on the left-hand side) depend on the diabatic angle and adiabatic electronic energies only. The adiabatic surfaces E1(R) and E2(R) are PESs obtained from clamped nuclei electronic structure calculations and Tn is the usual nuclear kinetic energy operator defined above.
Finding approximations for γ(R) is the remaining problem before a solution of the coupled nuclear Schrödinger equations can be attempted. Much of the current research in quantum chemistry is devoted to this determination. Once γ(R) has been found and the coupled equations have been solved, the final vibronic (vibration—i.e., nuclear motion—plus electronic) wave function in the diabatic approximation is
[edit] References
- ↑ F. T. Smith, Diabatic and Adiabatic Representations for Atomic Collision Problems, Physical Review, vol. 179, p. 111–123 (1969) DOI]
- ↑ W. Lichten, Resonant Charge Exchange in Atomic Collisions, Physical Review, vol. 131, p. 229–238 (1963) DOI


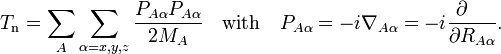
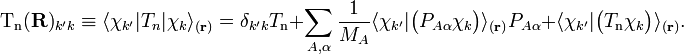
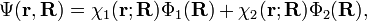
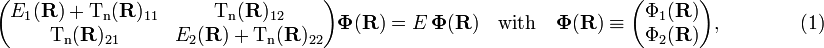
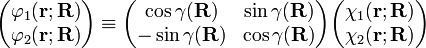
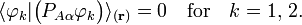
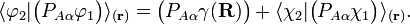
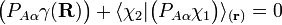
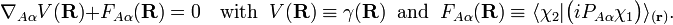
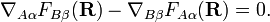
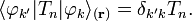
![\left[ \begin{pmatrix} T_\mathrm{n}+ \frac{E_{1}(\mathbf{R})+E_{2}(\mathbf{R})}{2} & 0 \\ 0 & T_\mathrm{n} + \frac{E_{1}(\mathbf{R})+E_{2}(\mathbf{R})}{2} \end{pmatrix} + \frac{E_{2}(\mathbf{R})-E_{1}(\mathbf{R})}{2} \begin{pmatrix} \cos2\gamma(\mathbf{R}) & \sin2\gamma(\mathbf{R}) \\ \sin2\gamma(\mathbf{R}) & -\cos2\gamma(\mathbf{R}) \end{pmatrix} \right] \tilde{\boldsymbol{\Phi}}(\mathbf{R}) = E \tilde{\boldsymbol{\Phi}}(\mathbf{R}).](../w/images/math/4/2/d/42d8a12a7d24ec4d30542d159f14b9af.png)