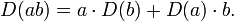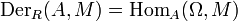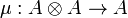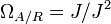Derivation (mathematics)
In mathematics, a derivation is a map which has formal algebraic properties generalising those of the derivative.
Let R be a ring and A an R-algebra (A is a ring containing a copy of R in the centre). A derivation is an R-linear map D from A to some A-module M with the property that
The constants of D are the elements mapped to zero. The constants include the copy of R inside A.
A derivation "on" A is a derivation from A to A.
Linear combinations of derivations are again derivations, so the derivations from A to M form an R-module, denoted DerR(A,M).
[edit] Examples
- The zero map is a derivation.
- The formal derivative is a derivation on the polynomial ring R[X] with constants R.
[edit] Universal derivation
There is a universal derivation (Ω,d) with a universal property. Given a derivation D:A → M, there is a unique A-linear f:Ω → M such that D = d·f. Hence
as a functorial isomorphism.
Consider the multiplication map μ on the tensor product (over R)
defined by 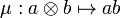 . Let J be the kernel of μ. We define the module of differentials
. Let J be the kernel of μ. We define the module of differentials
as an ideal in 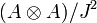 , where the A-module structure is given by A acting on the first factor, that is, as
, where the A-module structure is given by A acting on the first factor, that is, as 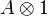 . We define the map d from A to Ω by
. We define the map d from A to Ω by
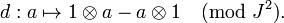 .
.
This is the universal derivation.
[edit] Kähler differentials
A Kähler differential, or formal differential form, is an element of the universal derivation space Ω, hence of the form Σi xi dyi. An exact differential is of the form dy for some y in A. The exact differentials form a submodule of Ω.
| |
Some content on this page may previously have appeared on Citizendium. |