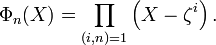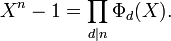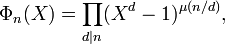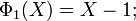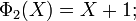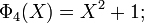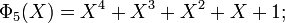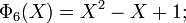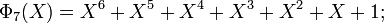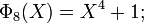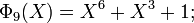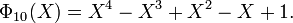Cyclotomic polynomial
From Knowino
In algebra, a cyclotomic polynomial is a polynomial whose roots are a set of primitive roots of unity. The n-th cyclotomic polynomial, denoted by Φn has integer cofficients.
For a positive integer n, let ζ be a primitive n-th root of unity: then
The degree of Φn(X) is given by the Euler totient function 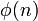 .
.
Since any n-th root of unity is a primitive d-th root of unity for some factor d of n, we have
By the Möbius inversion formula we have
where μ is the Möbius function.
[edit] Examples
| |
Some content on this page may previously have appeared on Citizendium. |