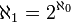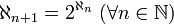Continuum hypothesis
In mathematics, the continuum hypothesis is the statement that any arbitrary infinite set of real numbers has either as many elements as there are real numbers or only as many elements as there are natural numbers (i.e., there is no intermediate size). This is equivalent to the statement that there are as many real numbers as there are elements in the smallest set which is larger than the set of natural numbers.
Since the set of real numbers (or the real line) is also called the continuum this can be shortly expressed as:
Any set of real numbers is either countable or equivalent to the continuum.
This statement was first made by Georg Cantor (1877) when he studied subsets of the real line. Cantor (who introduced sets and cardinal numbers) believed this to be true, but tried in vain to prove it.
From then on it stayed, for a long time, a prominent open mathematical problem to resolve. In 1900, David Hilbert included the continuum hypothesis as the first problem, therefore also called "first Hilbert problem", in his famous lecture on 23 problems for the twentieth century.
The first step towards a solution was done in 1938 by Kurt Gödel who showed that – in set theory including the axiom of choice – the (generalized) continuum hypothesis cannot be proved to be false (and thus is consistent with it). Only much later, in 1963, Paul J. Cohen showed that it cannot be proved, either. Hence the continuum hypothesis is independent of the usual (ZFC) axioms of set theory. It therefore constitutes an important, not artificially constructed, example for Gödel's Second Incompleteness Theorem.
Consequently, either the continuum hypothesis or, alternatively, some contradicting assumption could be added to the axioms of set theory. But since – in contrast to the situation with the axiom of choice – there is no heuristically convincing reason to choose one of these possibilities, the "working" mathematician usually makes no use of the continuum hypotheses, and if a result depends on it, then it is explicitly mentioned.
Of course, in axiomatic set theory, and especially in the theory of cardinal and ordinal numbers, the situation is different and the consequences of the various choices concerning the continuum hypothesis are extensively studied.
The generalized continuum hypothesis is a much stronger statement involving the initial sequence of transfinite cardinal numbers, and is also independent of ZFC.
In terms of the arithmetic of cardinal numbers (as introduced by Cantor) the continuum hypothesis reads
while the generalized continuum hypothesis is
[edit] Georg Cantor 1877
The continuum hypothesis appears in a memoir of Cantor (dated Halle a.S., 11th July 1877, and published 1878) in which he investigates sets of real numbers. He concludes with the following remark:
- Darnach würden die linearen Mannigfaltigkiten aus zwei Klassen bestehen von denen die erste alle Mannigfaltigkeiten in sich fasst, welche sich auf die Form: functio ips. ν (wo ν alle positiven ganzen Zahlen durchläuft) bringen lassen; während die zweite Klasse alle diejenigen Mannigfaltigkeiten in sich aufnimmt, welche auf die Form: functio ips. x (wo x alle reellen Werthe ≥0 und ≤1 annehmen kann) zurückführbar sind. Entsprechend diesen beiden Klassen würden daher bei unendlichen linearen Mannigfaltigkeiten nur zweierlei Mächtigkeiten vorkommen; die genaue Untersuchung dieser Frage verschieben wir auf eine spätere Gelegenheit.
Translated freely, this paragraph reads as follows:
- Hence the linear manifolds would consist of two classes of which the first contains all manifolds that can be written in the form: function of ν (where ν takes all positive integers); while the second class contains all those manifolds that have the form: function of x (where x takes all values ≥0 and ≤1). Hence, corresponding to these two classes, there would be only two cardinalities of infinite linear manifolds; the detailed investigation of this problem will be postponed on a later opportunity.
[edit] David Hilbert 1900
In his lecture on Mathematical problems, delivered before the International Congress of Mathematicians at Paris in 1900, David Hilbert states the continuum hypothesis as follows:
- 1. Cantors Problem von der Mächtigkeit des Continuums.
Zwei Systeme, d. h. zwei Mengen von gewöhnlichen reellen Zahlen (oder Punkten) heißen nach Cantor aequivalent oder von gleicher Mächtigkeit, wenn sie zu einander in eine derartige Beziehung gebracht werden können, daß einer jeden Zahl der einen Menge eine und nur eine bestimmte Zahl der anderen Menge entspricht. Die Untersuchungen von Cantor über solche Punktmengen machen einen Satz sehr wahrscheinlich, dessen Beweis jedoch trotz eifrigster Bemühungen bisher noch Niemanden gelungen ist; dieser Satz lautet:
Jedes System von unendlich vielen reellen Zahlen d. h. jede unendliche Zahlen- (oder Punkt)menge ist entweder der Menge der ganzen natürlichen Zahlen 1, 2, 3, ... oder der Menge sämmtlicher reellen Zahlen und mithin dem Continuum, d. h. etwa den Punkten einer Strecke aequivalent; im Sinne der Aeqivalenz giebt es hiernach nur zwei Zahlenmengen, die abzählbare Menge und das Continuum.
Aus diesem Satz würde zugleich folgen, daß das Continuum die nächste Mächtigkeit über die Mächtigkeit der abzählbaren Mengen hinaus bildet; der Beweis dieses Satzes würde mithin eine neue Brücke schlagen zwischen der abzählbaren Menge und dem Continuum.
In the English translation which was published in 1902:
- 1. Cantor's problem of the cardinal number of the continuum
Two systems, i. e., two assemblages of ordinary real numbers or points, are said to be (according to Cantor) equivalent or of equal cardinal number, if they can be brought into a relation to one another such that to every number of the one assemblage corresponds one and only one definite number of the other. The investigations of Cantor on such assemblages of points suggest a very plausible theorem, which nevertheless, in spite of the most strenuous efforts, no one has succeeded in proving. This is the theorem:
Every system of infinitely many real numbers, i. e., every assemblage of numbers (or points), is either equivalent to the assemblage of natural integers, 1, 2, 3,... or to the assemblage of all real numbers and therefore to the continuum, that is, to the points of a line; as regards equivalence there are, therefore, only two assemblages of numbers, the countable assemblage and the continuum.
From this theorem it would follow at once that the continuum has the next cardinal number beyond that of the countable assemblage; the proof of this theorem would, therefore, form a new bridge between the countable assemblage and the continuum.
Hilbert continues this problem, now known as the "First Hilbert Problem" by describing another unproven claim of Cantor (which he thought to likely be related), namely the statement that there is a well-order of the real numbers. This property, however, turned out to be a consequence of the axiom of choice.
[edit] Kurt Gödel 1947
In an essay (published 1947, after his proof and before Cohen's result) Kurt Gödel argued that even if the continuum hypothesis would turn out to be independent (as he expected) this would not imply that it cannot be solved at all:
- There might exist axioms so abundant in their verifiable consequences, shedding so much light upon a whole discipline, and furnishing such powerful methods for solving given problems (and even solving them, as far as that is possible, in a constructivistic way) that quite irrespective of their intrinsic necessity they would have to be assumed at least in the same sense as any well established physical theory.
He continues with a discussion of several arguments which support his position that the continuum hypothesis is likely to be wrong.
| |
Some content on this page may previously have appeared on Citizendium. |