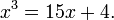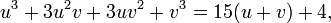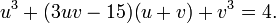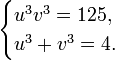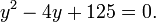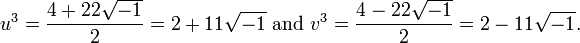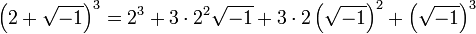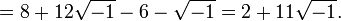Complex number/Advanced
[edit] Historical example
The need for complex numbers might have appeared for the first time during the sixteenth century, when Italian mathematicians like Scipione del Ferro, Niccolò Fontana Tartaglia, Gerolamo Cardano and Rafael Bombelli tried to solve cubic equations. Even for equations with three real solutions, the method they used sometimes required calculations with numbers whose squares are negative. A historical example of this is given below.
Here is such an example (with modern notation). Let us consider the equation
Cardano's method for solving it suggests looking for a solution by writing it as a sum x = u + v, where another condition on u and v is to be decided later. Recording this in the equation, we have, once the left member is expanded,
which can be written as
Now we recall that we did not completely specify u and v; we only required that x = u + v. Hence, we can choose another condition on u and v. We pick this condition to be 3uv − 15 = 0, or uv = 5, in order to simplify the above equation. This implies that u3 and v3 are numbers whose sum and product are given by
It follows from the second equation that v3 = 4 − u3. Substituting this in the first equation, we get u3(4 − u3) = 125. Hence we may find some values for u3 by solving the equation y(4 − y) = 125. Getting rid of the brackets and moving the number 125 to the left-hand side gives us the quadratic equation
Its discriminant is 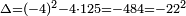 , which is negative, so that the quadratic equation has no real solution: the usual formulae giving the solutions require taking the square root of the discriminant, which is undefined here.
, which is negative, so that the quadratic equation has no real solution: the usual formulae giving the solutions require taking the square root of the discriminant, which is undefined here.
Well, let us be bold and write 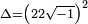 . Here, the symbol
. Here, the symbol 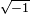 denotes an hypothetical number whose square would be − 1. At this stage, such a number has no meaning (squares of real numbers are always nonnegative), but we use it in a purely formal way. Using this symbol, we can write the "solutions" to the quadratic equation as
denotes an hypothetical number whose square would be − 1. At this stage, such a number has no meaning (squares of real numbers are always nonnegative), but we use it in a purely formal way. Using this symbol, we can write the "solutions" to the quadratic equation as
It remains to find cube roots of these "numbers". A straightforward calculation shows that 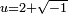 and
and 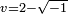 do the job. For instance, remembering the rule
do the job. For instance, remembering the rule 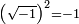 , we have
, we have
But now, going back to the original cubic equation, we get the real solution 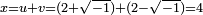 . One can verify it is indeed a solution, as
. One can verify it is indeed a solution, as 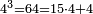 . And once this solution is found, it is easy to find the two other solutions
. And once this solution is found, it is easy to find the two other solutions 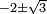 , which are also real.
, which are also real.
The fact that the formal calculations managed to give a real solution suggests that the "number" 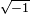 may have some sense. But to really give it a legitimate status, one has to construct a new set of numbers, containing the real numbers, but also other numbers whose squares may be negative real numbers. This will be the set of complex numbers. A rigorous construction of this set as pairs of real numbers was given much later by William Rowan Hamilton in 1837; this construction is explained in Complex number#Formal definition.
may have some sense. But to really give it a legitimate status, one has to construct a new set of numbers, containing the real numbers, but also other numbers whose squares may be negative real numbers. This will be the set of complex numbers. A rigorous construction of this set as pairs of real numbers was given much later by William Rowan Hamilton in 1837; this construction is explained in Complex number#Formal definition.