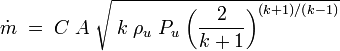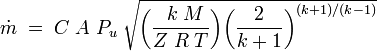Choked flow
The choked flow (often referred to as critical flow) of a flowing gas is a limiting point which occurs under specific conditions when a gas at a certain pressure and temperature flows through a restriction[1] into a lower pressure environment.
As the gas flows through the smaller cross-sectional area of the restriction, its linear velocity must increase. The limiting point is reached when the linear gas velocity increases to the speed of sound (sonic velocity) in the gas. At that point, the mass flow rate (mass per unit of time) of the gas becomes independent of the downstream pressure, meaning that the mass flow rate can not be increased any further by further lowering of the downstream pressure. The physical point at which the choking occurs (i.e., the cross-sectional area of the restriction) is sometimes called the choke plane. It is important to note that although the gas velocity becomes choked, the mass flow rate of the gas can still be increased by increasing the upstream pressure or by decreasing the upstream temperature.
The choked flow of gases is useful in many engineering applications because, under choked conditions, valves and calibrated orifice plates can be used to produce a particular mass flow rate. Choked flow in a de Laval nozzle as used in a rocket engine can be accelerated to supersonic linear velocities.
In the case of liquids, a different type of limiting condition (also known as choked flow) occurs when the Venturi effect acting on the liquid flow through the restriction decreases the liquid pressure to below that of the liquid vapor pressure at the prevailing liquid temperature. At that point, the liquid will partially "flash" into bubbles of vapor and the subsequent collapse of the bubbles causes cavitation. Cavitation is quite noisy and can be sufficiently violent to physically damage valves, pipes and associated equipment. In effect, the vapor bubble formation in the restriction limits the flow from increasing any further.[2][3]
Contents |
[edit] Conditions under which gas flow becomes choked
All gases flow from upstream higher pressure sources to downstream lower pressure environments. Choked flow occurs when the ratio of the absolute upstream pressure to the absolute downstream pressure is equal to or greater than:
- (1)
![\big[(k+1)/2 \big]^{\,k/(k-1)}](../w/images/math/1/9/4/194a68816a98d558b423ac27e41ff966.png)
where k is the specific heat ratio of the discharged gas (sometimes called the isentropic expansion factor and sometimes denoted as γ ).
For many gases, k ranges from about 1.09 to about 1.41, and therefore the expression in (1) ranges from 1.7 to about 1.9, which means that choked velocity usually occurs when the absolute upstream vessel pressure is at least 1.7 to 1.9 times as high as the absolute downstream pressure.
[edit] Mass flow rate equations for the choked flow of gases
When the gas velocity is choked, the equation for the mass flow rate in SI metric units is: [4][5][6][7]
where the terms are defined as in listed below. If the upstream gas density, ρu is not known directly, then it is useful to eliminate it using the Ideal gas law corrected for the real gas compressibility:
so that the mass flow rate is primarily dependent on the cross-sectional area A of the hole and the upstream pressure Pu, and only weakly dependent on the temperature T.
| where: | |
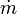
|
= mass flow rate, kg/s |
|---|---|
| C | = discharge coefficient, dimensionless (usually about 0.72) |
| A | = discharge hole area, m2 |
| k | = cp / cv = specific heat ratio of the gas |
| cp | = specific heat of the gas at constant pressure |
| cv | = specific heat of the gas at constant volume |
| ρu | = real gas upstream density, kg/m3 = 
|
| Pu | = absolute upstream pressure, Pa |
| M | = the gas molecular mass, kg/kmol (also known as the molecular weight) |
| R | = the universal gas law constant = 8314.5 Pa·m3/(kmole·K) |
| Tu | = absolute upstream gas temperature, K |
| Z | = the gas compressibility factor at Pu and Tu, dimensionless |
The technical literature can be confusing because many authors do not explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using Rs which only applies to a specific individual gas. The relationship between the two constants is Rs = R / M.
If the gas flow restriction is a leak hole in a closed pressure vessel or a gas pipeline, then the above equations calculate the initial instantaneous mass flow rate for the pressure and temperature existing in the source vessel when the leak first occurs. The initial instantaneous flow rate from a leak in a pressurized gas system or vessel is much higher than the average flow rate during the overall release period because the upstream pressure and the flow rate decrease with time as the vessel or pipeline empties. Calculating the flow rate versus time since the initiation of the leak is much more complicated, but more accurate. A comparison between two methods for performing such calculations is available online.[8]
Notes:
- The above equations are for a real gas.
- For an ideal gas, Z = 1 and ρu is the ideal gas density.
- kmole = 1000 moles
[edit] Minimum pressure ratio required for choked flow to occur
The minimum pressure ratios (also referred to as the critical pressure ratio) required for choked gas flow conditions to occur are presented in Table 1 for some industrial gases:
| Gas | k = cp/cv | Minimum Pu/Pd required for choked flow |
|---|---|---|
| Hydrogen | 1.410 | 1.899 |
| Methane | 1.307 | 1.837 |
| Propane | 1.131 | 1.729 |
| Butane | 1.096 | 1.708 |
| Ammonia | 1.310 | 1.838 |
| Chlorine | 1.355 | 1.866 |
| Sulfur dioxide | 1.290 | 1.826 |
| Carbon monoxide | 1.404 | 1.895 |
The above tabulated minimum pressure ratios were calculated by using the criterion that choked flow occurs when the ratio of the absolute upstream pressure to the absolute downstream pressure, Pu / Pd is equal to or greater than ![\big[(k+1)/2 \big]^{\,k/(k-1}](../w/images/math/d/4/2/d42056d7c7f3c41df776a79427c906f2.png) .
.
[edit] Thin-plate orifices
Experiments carried out by RG Cunningham (1951)[10][11] demonstrated that the assumption that choked flow could occur for gases flowing through thin, square-edged orifice plates is not correct. The flow continued to increase as the downstream pressure was reduced to as low as 0.2 of the upstream pressure.[12]
Cunningham’s work included tests using air and steam with the results and conclusions presented as tables, charts and formulas. Limited information was provided for the tests with steam.[12]
Critical flow can, however, be expected for thick orifice plates (i.e., plates with a thickness of at least 6 times the orifice hole diameter).[12]
[edit] References
- ↑ A valve, a convergent-divergent nozzle such as a de Laval nozzle, an orifice plate hole, a leak in a gas pipeline or other gas container, a rocket engine exhaust nozzle, etc.
- ↑ Scroll to discussion of liquid flashing and cavitation
- ↑ Search document for "Choked"
- ↑ 4.0 4.1 Perry's Chemical Engineers' Handbook, Sixth Edition, McGraw-Hill Co., 1984.
- ↑ Handbook of Chemical Hazard Analysis Procedures, Appendix B, Federal Emergency Management Agency, U.S. Dept. of Transportation, and U.S. Environmental Protection Agency, 1989. Handbook of Chemical Hazard Procedures
- ↑ "Risk Management Program Guidance For Offsite Consequence Analysis", U.S. EPA publication EPA-550-B-99-009, April 1999. Guidance for Offsite Consequence Analysis
- ↑ "Methods For The Calculation Of Physical Effects Due To Releases Of Hazardous Substances (Liquids and Gases)", PGS2 CPR 14E, Chapter 2, The Netherlands Organization Of Applied Scientific Research, The Hague, 2005. PGS2 CPR 14E (Scroll down to PGS2, download the PDF and then scroll to PDF pages 84-85)
- ↑ Calculating Accidental Release Rates From Pressurized Gas Systems
- ↑ Phillips Petroleum Company (1962). Reference Data For Hydrocarbons And Petro-Sulfur Compounds, Second Printing. Phillips Petroleum Company.
- ↑ R.G. Cunningham (1951). "Orifice Meters With Supercritical Flow". Trans. ASME 73: 625-630.
- ↑ Richard W. Miller (1996). Flow Measurement Engineering Handbook, Third Edition. McGraw Hill. ISBN 0-07-042366-0.
- ↑ 12.0 12.1 12.2 Flow through Orifice Plates in Compressible Fluid Service at High Pressure Drop
| |
Some content on this page may previously have appeared on Citizendium. |