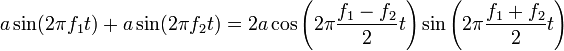Beat (acoustics)
In acoustics, a beat is an interference between two sounds of slightly different frequencies, perceived as periodic variations in volume whose rate is the difference between the two frequencies.
For example, if on an electric guitar the two treblest strings, B and E, are plucked, the ear can hear the two notes separately, and realizes that the total sound is even pleasant. If the E string is loosened more and more, to lower its frequency down to the B, for some time one will be able continue to hear two sounds, more or less harmonic. When the two strings have the same frequency, of course one sound will be heard; but just before there will be a strange effect: one sound will be heard, but its volume will appear to change over time, now louder and now quieter.
The reason of this phenomenon is tied to acoustics. If a graph is drawn to show the function corresponding to the total sound of two strings, it can be seen that maxima and minima are no longer constant as when a pure note is played, but change over time: when the two waves are nearly 180 degrees out of phase the maxima of each cancel the minima of the other, whereas when they are nearly in phase their maxima sum up, raising the perceived volume.
[edit] Physics of beat tones
It can be proven that the successive values of maxima and minima form a wave whose frequency equals the difference between the two starting waves. To demonstrate the simplest case, between two sine waves of equal amplitude:
If the two starting frequencies are quite close (usually differences of the order of few hertz), the frequency of the cosine of the right side of the expression above, that is (f1−f2)/2 is too slow to be perceived as a pitch. Instead, it is perceived as a periodic variation of the sine in the expression above (it can be said, the cosine factor is an envelope for the sine wave), whose frequency is (f1+f2)/2, that is, the average of the two frequencies. Since the amplitude of that wave is 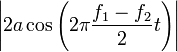 , which in the period of (f1−f2)/2 reaches values 2a and 0 twice, there will be two beats per such period. That is, the beating frequency is f1−f2, the difference between the two starting frequencies.
, which in the period of (f1−f2)/2 reaches values 2a and 0 twice, there will be two beats per such period. That is, the beating frequency is f1−f2, the difference between the two starting frequencies.
A physical interpretation is that when 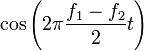 equals one, the two waves are in phase and they interfere constructively. When it is zero, they are out of phase and interfere destructively. Beats occour also in more complex sounds, or in sounds of different volumes, though calculating them mathematically is not so easy.
equals one, the two waves are in phase and they interfere constructively. When it is zero, they are out of phase and interfere destructively. Beats occour also in more complex sounds, or in sounds of different volumes, though calculating them mathematically is not so easy.
When the two waves are in unison f = 0 and as the difference between f1 and f2 increases, the speed increases until beyond a certain proximity (usu. about 15 Hz) beating becomes undetectable and a roughness is heard instead, after which the two pitches are perceived as separate. Beating can also be heard between notes that are near to, but not exactly, a harmonic interval, due to some harmonic of the first note beating with a harmonic of the second note. For example, in the case of perfect fifth, the third harmonic (i.e. second overtone) of the bass note beats with the second harmonic (first overtone) of the other note.
Musicians commonly use interference beats to objectively check tuning at the unison, perfect fifth, or other simple harmonic intervals.
[edit] Binaural beats
Binaural beats are heard when the right ear listens to a slightly different tone than the left ear. Here, the tones do not interfere physically, but are summed by the brain in the olivary nucleus. This effect is related to the brain's ability to locate sounds in three dimensions. There are also those who believe that the beats can be used to "entrain" the brain to a desired state.
| |
Some content on this page may previously have appeared on Citizendium. |