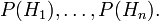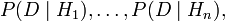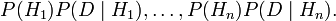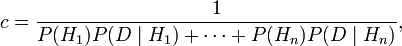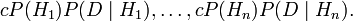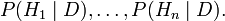Bayes Theorem
Bayes' Theorem is a theorem in probability theory named for Thomas Bayes (1702–1761).
It is used for updating probabilities by finding conditional probabilities given new data. This simplest case involves a situation in which probabilities have been assigned to each of several mutually exclusive alternatives H1, ..., Hn, at least one of which may be true. New data D is observed. The conditional probability of D given each of the alternative hypotheses H1, ..., Hn is known. What is needed is the conditional probability of each hypothesis Hi given D. Bayes' Theorem says
The use of Bayes' Theorem is sometimes described as follows. Start with the vector of "prior probabilities", i.e. the probabilities of the several hypotheses before the new data is observed:
Multiply these term-by-term by the "likelihood vector":
getting
The sum of these numbers is not (usually) 1. Multiply all of them by the "normalizing constant"
getting
The result is the "posterior probabilities", i.e. conditional probabilities given the new data:
In epidemiology, Bayes' Theorem is used to obtain the probability of disease in a group of people with some characteristic on the basis of the overall rate of that disease and of the probabilities of that characteristic in healthy and diseased individuals. In clinical decision analysis it is used for estimating the probability of a particular diagnosis given the base rate, and the appearance of some symptoms or test result.[1]
[edit] Calculations
[edit] References
- ↑ National Library of Medicine. Bayes Theorem. Retrieved on 2007-12-09.
| |
Some content on this page may previously have appeared on Citizendium. |