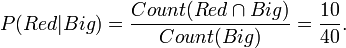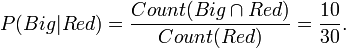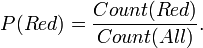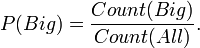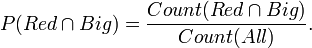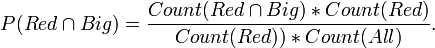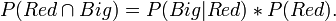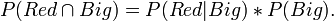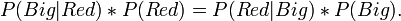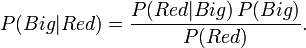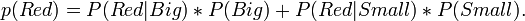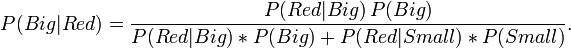Bayes' theorem
[edit] Bayesian Inference
Bayes' theorem is about conditional probabilities. Probability is about sets of outcomes. We start by assuming that these outcomes are equally likely. Suppose we have a bag full of balls, each ball is either red or blue. Each ball is also either Small or Big. Taking a ball from the bag is an outcome.
| Red | Blue | Total | |
|---|---|---|---|
| Small | |
|
|
| Big | |
|
|
| Total | |
|
|
The conditional probability of a ball taken from the bag being Red if we already know it is Big is 10/40. This is written,
These are conditional probabilities. P(Red | Big) means,
First I found that the ball was Big. What then is the probability of it being red.
The probabilities for a a ball being red P(Red) is,
Note that P(Red | Big) has no meaning by itself. Instead probability has two sets,
- The set of events that register success.
- The domain from which those events are taken.
Note that,
- P(Red) = P(Red | All).
The probabilities for a a ball being Big P(Big) is,
Now the probability of a ball being Red and Big 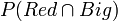 is,
is,
or,
so,
similarly,
so the result is,
This is Bayes' theorm usually written as,
it is also true that,
so,