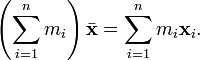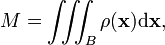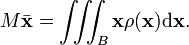Barycentre

From Knowino

This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 14 January 2011.

Pending changes are displayed on this page

Jump to: navigation, search

In geometry, the barycentre or centre of mass or centre of gravity^[1] of a system of particles or a rigid body is a point at which various systems of force may be deemed to act. The gravitational attraction of a mass is centred at its barycentre (hence the term "centre of gravity"), and the (classical) angular momentum of the mass resolves into components related to the rotation of the body about its barycentre and the angular movement of the barycentre.

The barycentre is located as an "average" of the masses involved. For a system of n point particles of mass $m i$ located at position vectors 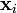$\mathbf{x}_i$ , the barycentre 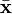$\bar{\mathbf{x}}$ is defined by

$\left( \sum_{i=1}^n m_i \right) \bar{\mathbf{x}} = \sum_{i=1}^n m_i \mathbf{x}_i . \,$

For a solid body B with mass density 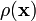$\rho(\mathbf{x})$ at position 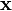$\mathbf{x}$ , with total mass

$M = \iiint_B \rho(\mathbf{x}) \mathrm{d}\mathbf{x} , \,$

the barycentre is given by

$M \bar{\mathbf{x}} = \iiint_B \mathbf{x} \rho(\mathbf{x}) \mathrm{d}\mathbf{x} . \,$

[edit] Notes

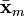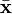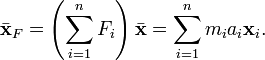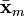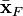↑ In physics, the centres of mass and gravity describe two slightly but importantly different concepts: While the centre of mass $\bar{\mathbf{x}}_m$ is defined like $\bar{\mathbf{x}}$ above as a spatial average of masses, the centre of gravity can be expressed similarly as a spatial average of the forces $F i$ involved: $\bar{\mathbf{x}}_F = \left( \sum_{i=1}^n F_i \right) \bar{\mathbf{x}} = \sum_{i=1}^n m_i a_i \mathbf{x}_i . \,$ Hence, $\bar{\mathbf{x}}_m$ and $\bar{\mathbf{x}}_F$ are generally only identical if the gravitational field (as expressed in terms of the acceleration $a i$ ) is constant for all 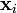$\mathbf{x}_i$ , such that $F i = a m i$ . 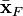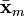The point on which forces may be deemed to act is then naturally $\bar{\mathbf{x}}_F$ and not $\bar{\mathbf{x}}_m$ .

Some content on this page may previously have appeared on Citizendium.

[0] In physics, the centres of mass and gravity describe two slightly but importantly different concepts: While the centre of mass $\bar{\mathbf{x}}_m$ is defined like $\bar{\mathbf{x}}$ above as a spatial average of masses, the centre of gravity can be expressed similarly as a spatial average of the forces $F i$ involved: $\bar{\mathbf{x}}_F = \left( \sum_{i=1}^n F_i \right) \bar{\mathbf{x}} = \sum_{i=1}^n m_i a_i \mathbf{x}_i . \,$ Hence, $\bar{\mathbf{x}}_m$ and $\bar{\mathbf{x}}_F$ are generally only identical if the gravitational field (as expressed in terms of the acceleration $a i$ ) is constant for all $\mathbf{x}_i$ , such that $F i = a m i$ . The point on which forces may be deemed to act is then naturally $\bar{\mathbf{x}}_F$ and not $\bar{\mathbf{x}}_m$ .

[1]

Barycentre

[edit] Notes

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox