Barometric formula
A barometric formula gives the pressure in a planetary atmosphere—usually the Earth's—as a function of height. Since the temperature and composition of the atmosphere are complicated functions of height, and because gravitation is an inverse function of distance to the center of the planet, a completely general barometric formula is very intricate.
However, two simplified formulas are in common use. The first is based on the assumption that temperature, gravitation, and composition are constant throughout the atmosphere. Further it is used that the atmosphere is an ideal gas. The equation thus obtained is a form of a Boltzmann distribution,
Here p(z) is the pressure at height z; z0 is a suitable reference height, often the surface of the planet and usually referred to as "base"; m is the mass of one mole of the atmospheric gas (note that the equation holds for a pure gas, if the atmosphere contains more than one compound a weighted-average mass is used); g is the constant gravitational acceleration; R is the molar gas constant; T is the absolute temperature (assumed to be independent of z).
The second barometric formula is based on the same assumptions as the first, the only generalization being that the temperature is taken to be linear in height with a slope L, the atmospheric lapse rate. The equation is
In practical applications,[1] the lowest part of the Earth's atmosphere is divided in 7 layers that start (above sea level) at:
- 0, 11, 20, 32, 47, 51, 71 km'
and end at 84.8520 km' (86.000 km), where the unit km' is the geopotential kilometer, which is nearly equal to the geometric (SI) kilometer. For each layer the second equation may be applied with values for T and L appropriate for that layer. Values of T and L are listed in the given reference.
Contents |
[edit] Proof
The two equations follow by integration of a simple differential equation that holds for the pressure of an ideal gas in a constant gravitational field.
[edit] Differential equation
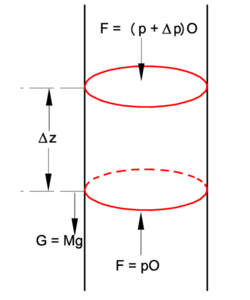
In the figure we see a stationary pillbox at arbitrary position z in a cylinder filled with an atmospheric gas that, for obvious reason, we call "air". The pillbox is pushed upward by a pressure force pO, and pulled down by gravitation that acts with the force G equal to the total mass M of air in the pillbox times the gravitational acceleration g. Also the air pressure (p+ Δp)O at the top acts downward. Forces upward are positive, downward negative, and since the total force is zero (no motion of air), we have
The total mass in the pillbox is the molar density ρ times the molar mass m times the volume of the pillbox Δz·O
Hence
Noting that the molar density is the number of moles per volume, we get for an ideal gas,
Assuming that the gas in the pillbox is ideal and of absolute temperature T, we get the equation
Taking the limit of infinitesimally small Δ and remembering that the derivative of the natural logarithm is given by
we arrive at the differential equation (the hydrostatic equation):
[edit] Constant temperature
The master equation (1) can be solved by integrating the left hand side from p(z0) ≡ p0 to p(z) and the right hand side from z0 to z. Hence
where we recall that
Taking the exponent (the inverse function of the natural logarithm) of both sides of equation (2) we get
This distribution is known in statistical thermodynamics as a Boltzmann distribution.
[edit] Temperature linear in height
We assumed in the previous subsection that T is constant throughout the cylinder, which makes the equation useful for cases where there is no temperature gradient, i.e., cases where the temperature at the top of the cylinder is equal to the temperature at the bottom. The master equation (1) can be modified for the case of a constant temperature gradient (constant lapse rate). That is, we make in equation (1) the substitution
The modified equation is:
Substitute
The integral on the right hand side becomes
We already saw that the integral on the left hand side is the logarithm of p/p0. hence
[edit] Reference
- ↑ U.S. Standard Atmosphere, 1976. A report by the National Oceanic and Atmospheric Administration, The National Aeronautic and Space Administration, and The U.S. Air Force Online


![p(z) = p(z_0) \; \exp\left[ - \frac{mg}{RT} (z-z_0)\right].](../w/images/math/9/6/b/96b9f0aefcb84db69424336a3ca2b24d.png)
![p(z) = p(z_0) \; \left[ \frac{T}{T + L (z-z_0)}\right]^{mg/(LR)}.](../w/images/math/2/9/7/2978ab5c171fd8dd5a737c3d40fbed51.png)
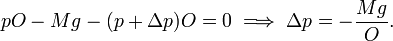
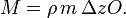
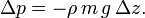
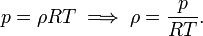
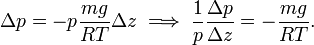
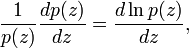

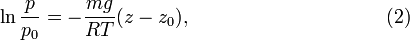
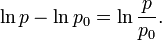
![\frac{p}{p_0} = \frac{\exp\left[- \frac{mg}{RT} z\right]}{\exp\left[- \frac{mg}{RT} z_0\right]} \;\Longleftrightarrow\; p = p_0 \, \exp\left[ - \frac{mg}{RT}(z-z_0) \right].](../w/images/math/8/a/0/8a02d109d9c9e3686bf3b9fad9b2d59f.png)
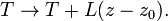
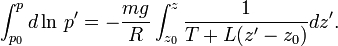
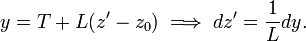
![- \frac{mg}{L R} \int^{T+L(z-z_0)}_T \frac{dy}{y} = - \frac{mg}{L R} \ln \frac{T+L(z-z_0)}{T} = \ln\;\left[ \frac{T}{T+L(z-z_0)} \right]^{\frac{mg}{L R}}.](../w/images/math/a/f/6/af67495da3c6f6868f7038923dfa634c.png)
![\frac{p}{p_0} = \left[ \frac{T}{T+L(z-z_0)} \right]^{\frac{mg}{L R}}.](../w/images/math/9/0/b/90bf104a7826968af326442063fd1c72.png)