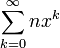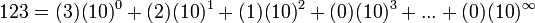Adder (electronics)

An adder is a digital circuit designed to perform integer addition in the Arithmetic Logic Unit on board a computer. These circuits are fundamental to the operation of a computer and have an analog in traditional pencil-and-paper addition.

Integers can be represented by the sum of a series from 0 to infinity.

• Where n is an integer from zero to (base - 1)
• Where x is an integer equal to the base value.

Example, base x = 10, then

An adder performs a binary operation (two operands) where the n of one power in integer A is added to the n of the same power in integer B. This produces two outputs, a sum, and a carry. The carry is always equal to (sum - (base - 1)). The carry is then added to the sum of the next power's sum, and so on. This represents what is known as a full adder. Each addition operation performed is known as a half adder. Chain a number of half adders together, and a full adder emerges.

[edit] The half adder

Computers operate in base-2, or binary. To the computer, a presence of electrons represents a 1 and a lack of electrons represents a 0. A computer's ALU (Arithmetic Logic Unit) consists of a variety of circuits that perform different operations, the adders are composed mostly of half adders. The truth table associated with a half adder can be derived by knowing the internal functions of the half adder. The half adder consists of an XOR (exclusive OR) gate and an (AND) gate connected to the same input lines. Physically, the voltage potential is equal on both branches from the input lines to their associated gates. The (XOR) gate will output the sum bit, and the (AND) gate will output the carry bit.

Truth table of the half adder
inputs	sum	carry
0+0	0	0
0+1	1	0
1+0	1	0
1+1	0	1

Some content on this page may previously have appeared on Citizendium.