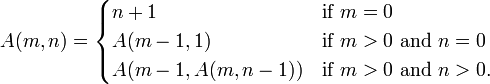Ackermann function
In computability theory, the Ackermann function or Ackermann-Péter function is a simple example of a computable function that is not primitive recursive. The set of primitive recursive functions is a subset of the set of general recursive functions. Ackermann's function is an example that shows that the former is a strict subset of the latter. [1].
Contents |
[edit] Definition
The Ackermann function is defined recursively for non-negative integers m and n as follows::
[edit] Rapid growth
Its value grows rapidly; even for small inputs, for example A(4,2) contains 19,729 decimal digits [2].
[edit] Holomorphic extensions
The lowest Ackermann functions allow the extension to the complex values of the second argument. In particular,
- A(0,z) = z + 1
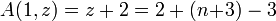
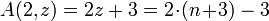
The 3th Ackermann function is related to the exponential on base 2 through
The 4th Ackermann function is related to tetration on base 2 through
- A(4,z) = tet2(z + 3) − 3
which allows its holomorphic extension for the complex values of the second argument. [3]
For n > 4 no holomorphic extension of A(n,z) to complex values of z is yet reported.
[edit] References
- ↑ Wilhelm Ackermann (1928). "Zum Hilbertschen Aufbau der reellen Zahlen". Mathematische Annalen 99: 118–133. DOI:10.1007/BF01459088. Research Blogging.
- ↑ Decimal expansion of A(4,2)
- ↑ D. Kouznetsov. Ackermann functions of complex argument. Preprint ILS, 2008, http://www.ils.uec.ac.jp/~dima/PAPERS/2008ackermann.pdf
| |
Some content on this page may previously have appeared on Citizendium. |