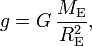Acceleration due to gravity
An object with mass m near the surface of the Earth experiences a downward gravitational force of magnitude mg, where g is the acceleration due to gravity. The quantity g has the dimension of acceleration, m s−2, hence its name.
Newton's gravitational law gives the following formula for g,
where G is the universal gravitational constant,[1] G = 6.67384 × 10−11 m3 kg−1 s−2, ME is the total mass of the Earth, and RE is the radius of the Earth. This equation gives a good approximation, but is not exact. Deviations are caused by the centrifugal force due to the rotation of the Earth around its axis, non-sphericity of the Earth, and the non-homogeneity of the composition of the Earth. These effects cause g to vary roughly ± 0.01 around the value 9.8 m s−2 from place to place on the surface of the Earth. The quantity g is therefore referred to as the local gravitational acceleration.
The 3rd General Conference on Weights and Measures (Conférence Générale des Poids et Mesures, CGPM) defined in 1901 a standard value denoted as gn.[2] [3] The value of the standard acceleration due to gravity gn is 9.80665 m s−2. This value of gn was the conventional reference for calculating the now obsolete unit of force, the kilogram force.
[edit] References
- ↑ Source: CODATA 2006, retrieved 7/9/11 from NIST website
- ↑ The International System of Units (SI), NIST Special Publication 330, 2001 Edition (pdf page 29 of 77 pdf pages)
- ↑ Bureau International des Poids et Mesures (Brochure on SI, pdf page 51 of 88 pdf pages) From the website of the Bureau International des Poids et Mesures