1-f noise
1 / f noise, or more accurately 1 / fα noise, is a signal or process with a power spectral density proportional to 1 / fα,
where f is the frequency. Typical use of the term focuses on noises with exponents in the range 0 < α < 2, that is, fluctuations whose structure falls in-between white (α = 0) and brown (α = 2) noise. Such "1 / f-like" noises are widespread in nature and a source of great interest to diverse scientific communities.
The "strict 1 / f" case of α = 1 is also referred to as pink noise, although the precise definition of the latter term[1] is not a 1 / f spectrum per se but that it contains equal power per octave, which is only satisfied by a 1 / f spectrum. The name stems from the fact that it lies in the middle between white (1 / f0) and red (1 / f2, more commonly known as Brown or Brownian) noise[2].
The term flicker noise is sometimes used to refer to 1 / f noise, although this is more properly applied only to its occurrence in electronic devices. Mandelbrot and Van Ness proposed the name fractional noise (sometimes since called fractal noise) to emphasise that the exponent of the spectrum could take non-integer values and be closely related to fractional Brownian motion, but the term is very rarely used.
Contents |
[edit] Description
In the most general sense, noises with a 1 / fα spectrum include white noise, where the power spectrum is proportional to 1 / f0 = constant, and Brownian noise, where it is proportional to 1 / f2. The term black noise is sometimes used to refer to 1 / fα noise with an exponent α > 2.
[edit] Pink noise
Pink noise is a term used in acoustics and engineering for noise which has equal power per octave or similar log-bundle[1]. That is, if we consider all the frequencies in the range [f,λf], the total power should depend only on λ and not on f. We can see that a strict 1 / f spectrum satisfies this if we calculate the integral,
[edit] Relationship to fractional Brownian motion
The power spectrum of a fractional Brownian motion of Hurst exponent H is proportional to: 1 / f(2H + 1)
[edit] References
- ↑ 1.0 1.1 Federal Standard 1037C and its successor, American National Standard T1.523-2001.
- ↑ Confusingly, the term "red noise" is sometimes used instead to refer to pink noise. In both cases the name springs from analogy to light with a 1 / fα spectrum: as α increases, the light becomes darker and darker red.
| |
Some content on this page may previously have appeared on Citizendium. |


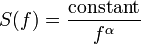
![\int_{f}^{\lambda f} \frac{1}{f'}\mathrm{d}f' = \left[ \log f' \right]_{f}^{\lambda f} = \log(\lambda f) - \log f = \log\lambda + \log f - \log f = \log\lambda.](../w/images/math/6/0/3/6033583f5652a9973713f6e1919f79dc.png)