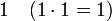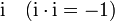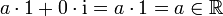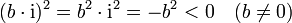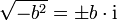Imaginary number
The imaginary numbers are a part of the complex numbers. Every complex number can be written as the sum a+bi of a real number a and an imaginary number bi (with real numbers a and b, and the imaginary unit i). Since the square (bi)2 = −b2 of an imaginary number is a negative real number, the imaginary numbers are just the square roots of the negative real numbers. In the complex plane the imaginary numbers lie on the imaginary axis, perpendicular to the real axis.
However, sometimes the term "imaginary" is used more generally for all non-real complex numbers, i.e., all numbers with non-vanishing imaginary part (b not 0), are called "imaginary". In this case, the more specific complex numbers bi (with vanishing real part a=0) are called pure(ly) imaginary.
Remark:
The names "imaginary" and "complex" number are of historical origin,
just as the other names for numbers
— "rational", "irrational", and "real" — are.
Thus they must not be interpreted literally,
and no mathematical or philosophical conclusions may be drawn from them.
Numbers: complex, real and imaginary
Every complex number is the real linear combination of the real unit
and the imaginary unit
that is, a complex number can uniquely be written as
In this expression, the real number a is called the real part and the real number b the imaginary part of the complex number a+bi.
While (real) multiples of 1 (i.e., complex numbers with imaginary part 0) are (identified with) the real numbers:
the (real) multiples of i (i.e., complex numbers with real part 0)
are the imaginary numbers, or pure imaginary numbers, depending on usage.
Characterization
The square of an imaginary number
is a negative real number.
Conversely, the (two) square roots of a negative real number
are imaginary numbers.
Origin
Imaginary numbers first occurred — as square roots of negative numbers —
when the formula for solving cubic equations was found.
It turned out that using square roots of negative numbers
— which "do not exist" and therefore are only "imagined" —
as purely formal expressions may lead to valid "existing" solutions in ("real") numbers (see Complex number/Advanced).
Moreover, numbers which are "composed" from real and imaginary numbers are not simple but "complex".
| |
Some content on this page may previously have appeared on Citizendium. |