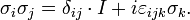Pauli spin matrices
From Knowino
This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 20 December 2010.
The Pauli spin matrices (named after physicist Wolfgang Ernst Pauli) are a set of unitary Hermitian matrices which form an orthogonal basis (along with the identity matrix) for the real Hilbert space of 2 × 2 Hermitian matrices and for the complex Hilbert spaces of all 2 × 2 matrices. They are usually denoted:
Algebraic properties
For i = 1, 2, 3:
Commutation relations
The Pauli matrices obey the following commutation and anticommutation relations:
- where
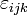 is the Levi-Civita symbol, δij is the Kronecker delta, and I is the identity matrix.
is the Levi-Civita symbol, δij is the Kronecker delta, and I is the identity matrix.
The above two relations can be summarized as:
| |
Some content on this page may previously have appeared on Citizendium. |
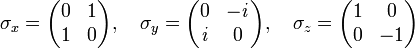
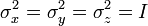
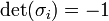
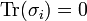
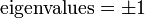
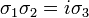
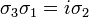
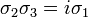
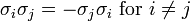
![\begin{matrix}
[\sigma_i, \sigma_j] &=& 2 i\,\varepsilon_{i j k}\,\sigma_k \\[1ex]
\{\sigma_i, \sigma_j\} &=& 2 \delta_{i j} \cdot I
\end{matrix}](images/math/8/8/9/8894f47603f2c48c392fd00f5fcada72.png)