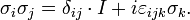Pauli spin matrices
From Knowino
The Pauli spin matrices (named after physicist Wolfgang Ernst Pauli) are a set of unitary Hermitian matrices which form an orthogonal basis (along with the identity matrix) for the real Hilbert space of 2 × 2 Hermitian matrices and for the complex Hilbert spaces of all 2 × 2 matrices. They are usually denoted:
[edit] Algebraic properties
For i = 1, 2, 3:
[edit] Commutation relations
The Pauli matrices obey the following commutation and anticommutation relations:
- where
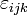 is the Levi-Civita symbol, δij is the Kronecker delta, and I is the identity matrix.
is the Levi-Civita symbol, δij is the Kronecker delta, and I is the identity matrix.
The above two relations can be summarized as:
| |
Some content on this page may previously have appeared on Citizendium. |


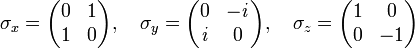
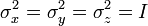
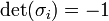
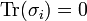
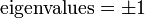
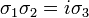
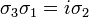
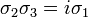
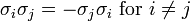
![\begin{matrix}
[\sigma_i, \sigma_j] &=& 2 i\,\varepsilon_{i j k}\,\sigma_k \\[1ex]
\{\sigma_i, \sigma_j\} &=& 2 \delta_{i j} \cdot I
\end{matrix}](images/math/8/8/9/8894f47603f2c48c392fd00f5fcada72.png)