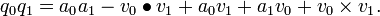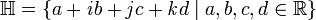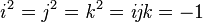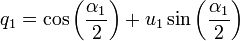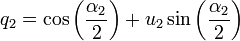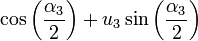Quaternions
Quaternions are numbers of the form a + bi + cj + dk, where a, b, c and d are real numbers and each of i,j,k denotes a number-like entity satisfying i2 = − 1, j2 = − 1 and k2 = − 1 respectively. Of course, since the square of any real number is nonnegative, none of the entities i, j or k can be a real number. At first glance, it is not even clear whether such objects can exist in any meaningful sense: for example, can we sensibly associate with i, j and k natural operations such as addition and multiplication? As it happens, we can define such mathematical operations in a consistent and sensible way and, perhaps more importantly, the resulting system provides mathematicians, physicists, and engineers with a powerful approach to expressing parts of these sciences in a convenient and natural-feeling way.
Contents |
Historical context
The need for quaternions became apparent after the successful introduction of complex numbers into mathematics. These numbers made it possible to add, subtract, multiply and divide tuplets - points in the plane - just like one can do with real numbers. The search for a larger system, where one can similarly deal with triplets - points in 3-dimensional space - became the natural next step. It turned out, however, that there is no way triplets of real numbers can form such a system. The breakthrough came with Sir William Rowan Hamilton, when he realized that quadruples would work. He famously inscribed their defining equation on Broom Bridge in Dublin when walking with his wife on 16 October 1843.
Working with quaternions
Quaternion arithmetic is surprisingly straightforward. The main difficulty is that commutativity in multiplication is lost — for two quaterions q1 and q2 we cannot, in general, expect that q1q2 = q2q1.
For purposes of computation, it's often convenient to write a quaternion q = a + bi + cj + dk in the form q = a + v and treat v as an ordinary 3-dimensional vector (b,c,d).
Basic operations
Quaternion addition is straightforward,
- (a0 + b0i + c0j + d0k) + (a1 + b1i + c1j + d1k) = (a0 + a1) + (b0 + b1)i + (c0 + c1)j + (d0 + d1)k.
The result is again a quaternion.
Multiplication is a little more complicated.
Given the two quaternions q0 = a0 + b0i + c0j + d0k = a0 + v0 and q1 = a1 + b1i + c1j + d1k = a1 + v1, their product is given by
Geometric interpretations
Both the real numbers and the complex numbers can be given various geometric interpretations. It's not surprising that their arguably most natural extension, the quaternions, can be given several geometric interpretations as well.
Like a real number can be interpreted as a point in 1-dimensional space, and a complex number can be interpreted as a point in 2-dimensional space, a quaternion may be interpreted as a point in 4-dimensional space.
Also, a quaternion can be viewed as a transformation (function) acting on 3-dimensional space, similar to the way a complex number may represent a 2-dimensional rotation and/or dilation.
Also, a quaternion can be viewed as a transformation (function) acting on 4-dimensional space, similar to the way a complex number may represent a 2-dimensional affine transformation.
There are other ways to interpret quaternions as well.
Algebraic closure
Formal definition
Definition & basic operations
The quaternions, 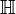 , form a four-dimensional normed division algebra over the real numbers.
, form a four-dimensional normed division algebra over the real numbers.
They are a non-commutative extension of the real numbers. They were first described by Sir William Rowan Hamilton in 1843.
Properties
Applications
Quaternions have many applications, including in computer graphics, but have during their history proved comparatively unpopular, with vectors being preferred instead, especially among engineers.
In 3-dimensional space, any sequence of rotations around any number of different axes intersecting the origin can be represented by a single rotation — the set of all such rotations form a group.
The set of unit quaternions under quaternion multiplication also form a group, which can be used to model the three-dimensional rotation group.
A unit quaternion then represents a rotation, multiplying two quaternions represents performing two rotations in sequence, the resulting quaternion represents the equivalent single rotation.
Given an ordinary 3-dimensional vector u1 of unit length and an angle α1, the quaternion
then represents a rotation over an angle α1 around the axis defined by the unit vector u1.
Given a similarly defined quaternion
one can — using the formulas for quaternion multiplication — compute their product quaternion q1q2, which can again be written in the form
for some angle α3 and some unit vector u3.
It represents a rotation over an angle α3 around the axis defined by the unit vector u3
Note that each of the quaternion units (i, j, k) in this model represents a 180-degree rotation, and the quaternion −1 represents a full rotation. The quaternion representation thus keeps track of rotations, in addition to a fermionic phase factor of ±1.
See also
Related topics
References
- Henry Baker. Quaternion references. Electronic document.
- Simon Altmann (2005). Rotations, Quaternions, and Double Groups. Dover Publications. ISBN 978-0486445182. (First edition appeared in 1977).
External links
- Quaternion at MathWorld
| |
Some content on this page may previously have appeared on Citizendium. |