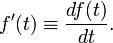Talk:Sine
Equation numbering is screwed up. First two equations are numbered on the right (by me on CZ). Later equations are numbered on the left with too small a space; eq numbers (1), (2) and (13), (14) are duplicate.--Paul Wormer 04:01, 13 June 2011 (EDT)
- Indeed. So, what to do? Is it at all a good idea to use a lot of numbered formulas in encyclopedic article? And of course, it makes the article hardly editable; here we cannot use LaTeX service of automatic numbering. We should either use numbers very sparingly, or make them hierarchical; for example, the formulas in Sect.2.1 "Definition" should be (2.1.1), (2.1.2), ... rather than (1), (2), ... Your opinion? --Boris Tsirelson 13:55, 13 June 2011 (EDT)
- Apart from the presentation, what do you think of the contents? I wrote section 1 [so mind your words :-)], but what about the bracketing and such, is that important, aren't there there any more relevant facts to be mentioned? --Paul Wormer 03:56, 14 June 2011 (EDT)
- Yes, it is somewhat strange. If you'll rewrite it, I'll be glad. By the way, Cauchy-Kowalevski theorem is completely irrelevant. --Boris Tsirelson 09:43, 14 June 2011 (EDT)
Contents |
Moved from the article
Several sections below are moved hereto from the article. Maybe some day this content will be used for "Sine/advanced" or other appropriate articles. --Boris Tsirelson 14:15, 20 June 2011 (EDT)
Definition by differential equations
One could say that the geometrical approach assumes the properties of sin and cos rather than deduce them. These assumptions are masked as the geometric axioms. However, as we will now show, the deduction of properties of trigonometric functions does not require axioms of geometry. Properties of sin and cos do not depend, for example, on the acceptance or rejection of the Euclid's parallel axiom. The functions sin and cos can be defined algebraically, and their properties can be deduced, not postulated. The basic elements of such a deduction are outlined below.
The definitions of derivative and integral do not depend on trigonometric functions, and the basic properties of integrals and derivatives (in particular the Cauchy-Kowalevski theorem of existence and uniqueness of the solution of the Cauchy problem) can be deduced without reference to sin, cos, or any axioms of Euclidean geometry. Therefore, a natural and consistent way of defining the functions sin and cos is via differential equations.
We will indicate the first derivative of a function with respect to its variable by a prime:
Definition
The functions sin and cos are solutions of the following system of equations
- (1)
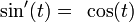
- (2)
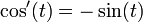
with conditions
- (3)
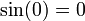
- (4)
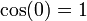
Usually, it is assumed that the independent variable t is real; in that case, the values of the functions sin and cos are also real numbers. However, the definition above can be used for complex numbers too.
The present definition does not imply additional concepts about angles and sums of angles; and does not require the Pythagorean theorem or even the parallel axiom of Euclidean geometry. Furthermore the definition does not refer to the concept of the number Pi (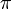 ) and therefore can be used for the definition of
) and therefore can be used for the definition of 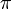 . But,
one pays for this by having to deduce the properties of sin and cos from the system (1)–(4).
. But,
one pays for this by having to deduce the properties of sin and cos from the system (1)–(4).
Sum of squares
Consider the function
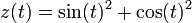 . From equations (1) and (2) it follows that
. From equations (1) and (2) it follows that
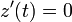 , i.e.,
, i.e.,
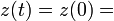 constant . Evaluation of this constant from equations (2) and (3) gives
constant . Evaluation of this constant from equations (2) and (3) gives
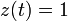 for all
for all
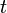 , i.e.,
, i.e.,
- (5)
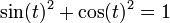
In this article, the superscript as indicator of exponentiation is always written last to specify the argument, avoiding the confusions. [1]
For the equation (5) it follows, that for all real values of t the functions sin(t) and cos(t) are bounded:
- (6)
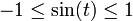
- (7)
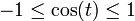
These properties allow efficient bracketing of functions sin and cos.
Bracketing
Consider sin(x) and cos(x) in the case x > 0. From equation (1) it follows that sin'(x) ≤ 1 . Integration of the last inequality with respect to x from 0 to t gives: sin(t) − sin(0) < t. Using equation (3) we write
- (8) sin(t) < t .
Rewrite (8) as − t < − sin(t) and apply equation(2):
- − t < cos'(t)
Integrating this inequality with respect to t from 0 to x gives:
- − x2 / 2 < cos(x) − cos(0)
Using equation(4) gives
- (9) 1 − x2 / 2 < cos(x) < 1
The last "<" just follows from equation (7). Using equation (1) gives
- (10) 1 − x2 / 2 < sin'(x) < 1
Integrating equation (12) with respect to x from 0 to t gives
- (11) t − t3 / 6 < sin(t) < t
Rewrite it as
- − t < − sin(t) < − t + t3 / 6
and apply equation (2):
- − t < cos'(t) < − t + t3 / 6
Integrating this equation with respect to t from 0 to x gives
- − x2 / 2 < cos(x) − cos(0) < − x2 / 2 + x3 / 6
- (12) 1 − x2 / 2 < cos(x) < 1 − x2 / 2 + x4 / 24
Continuing this exercise, one can obtain more and more narrow bounds for values of sin and cos.
However, even equations (9,12) are sufficient to see that both both sin and cos remain positive while, the argument is within (0,1) range. This property is used below to reveal periodicity of these funcitons.
Mathematical induction
Applying the mathematical induction, it is possible to show that for positive integer N
- (13)
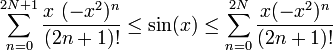
- (14)
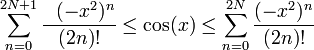
and equality takes place only at x = 0.
Is cos always larger than sin?
Consider the range 0 < t < P such that both sin(t) and cos(t) are positive; let P be exact upper bound of such interval. Within this interval, sin is monotonously increasing, and cos is monotonously decreasing. Therefore, there exist one and only one solution p of the equation
- (13) sin(p) = cos(p)
Let us estimate value of this solution.
Consider the special case, substitute x = 1 into equation(13) and t = 1 into equation(11). This gives
- cos(1) < 1 − 1 / 2 + 1 / 24 = 13 / 24
- sin(1) > 1 − 1 / 6 = 5 / 6 = 20 / 24
In such a way,
- (14) sin(1) > cos(1)
hence,
- (15) p < 1.
Substitute x = 3 / 4 into equation (11); this gives
- (16) cos(3 / 4) > 1 − (3 / 4)2 / 2 = 23 / 32
- (17) cos(3 / 4)2 > 529 / 1024 > 1 / 2
From equation (5) it follows that
- (18) sin(3 / 4)2 = 1 − cos(3 / 4)2 < 1 − 529 / 1024 < 1 / 2
- (19) sin(3 / 4)2 < cos(3 / 4)2
Both sin and cos are positive in the range (0,1); and, therefore,
- (20) sin(3 / 4) < cos(3 / 4)
Therefore,
- (21) 3 / 4 < p < 1.
Symmetry and sense of number P
Change of variables t to − t and replacement sin to − sin keeps the system (1)-(4) invariant. This means that
- (22) sin( − t) = − sin(t)
- (23) cos( − t) = cos(t)
Consider replacement t to p − t, cos to sin, and sin to cos. Due to equation (13), such a replacement preserves the equations (1-4); therefore,
- (24) sin(p − t) = cos(t)
- (25) cos(t − p) = sin(t)
Then, P = 2p, and
- (26) sin(t + P) = cos(P)
- (27) cos(t + P) = − sin(P)
It follows, that functions sin and cos are periodic; and
- (30) 2π = 4P = 8p
is period. The deduction above can be used as definition of number π. In such a way, π appears as half of period of functions which are solutions of equations (1,2).
For definition of π, equations (1,2) are sufficient: due to the linearity of equations and the translational invariance, conditions (3,4) do not affect the period; all the solutions with different conditions at zero have the same period.
From estimate (21) it follows that
- (31)3 < π < 4
The improvement of this estimate using the expansions (13), (14) is possible but computationally non-efficient. The efficient algorithms for evaluation of π are mentioned in the spacial article about Pi. Usually, the efficient algorithms require more efforts for the deduction.
Notes
- ↑
Some authors implicitly define also functions with superscript,
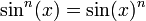 and cosn(x) = cos(x)n.
However, such a notation leads to confusions as soon as one needs to consider the inverse function
(for a function
and cosn(x) = cos(x)n.
However, such a notation leads to confusions as soon as one needs to consider the inverse function
(for a function  , it is common to use notation
, it is common to use notation  for inverse function, such that
for inverse function, such that 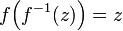 )
or multiple combination of functions, for example:
sin − 1(x) = arcsin(x);
)
or multiple combination of functions, for example:
sin − 1(x) = arcsin(x);
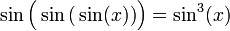 .
.
End of the content moved hereto from the article