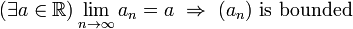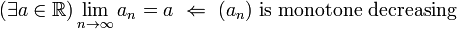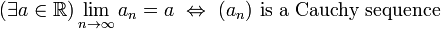Necessary and sufficient
Contents |
In mathematics, the phrase
"necessary and sufficient"
is frequently used, for instance,
in the formulation of theorems,
in the text of proofs when a step has to be justified,
or when an alternative version for a definition is given.
To say that a statement is "necessary and sufficient" to another statement
means that the statements are either both true or both false.
Another phrase with the same meaning is "if and only if" (abbreviated to "iff").
In formulae "necessary and sufficient" is denoted by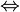 
.
There are also some special terms used to indicate the presence of a necessary and sufficient condition, usually used for statements of special significance:
A criterion is a proposition
that expresses a necessary and sufficient condition for a statement to be true.
The term is mostly used in cases
where this condition is easier to check than the statement itself.
While — in the strict sense of the word —
the condition given in a criterion has to be necessary and sufficient,
the term is sometimes (mostly out of tradition)
also used for conditions which are only sufficient.
A characterization of a mathematical object, a class of objects, or a property, is an alternative description equivalent to a previously given definition, i.e., a necessary and sufficient condition. This term is mainly used in cases where the condition is mathematically interesting and provides new insight.
Necessary and sufficient
A statement A is
- "a necessary and sufficient condition",
or shorter,
- "necessary and sufficient"
for another statement B if it is both
- a necessary condition
and
- a sufficient condition
for B.
Necessary
The statement
- A is a necessary condition for B
or shorter
- A is necessary for B
means precisely the same as each of the following statements:
- If A is false then B cannot be true
- B is false whenever A does not hold
- B implies A
Sufficient
The statement
- A is a sufficient condition for B
or shorter
- A is sufficient for B
means precisely the same as each of the following statements:
- A implies B
- B holds whenever A is true
Examples
For a sequence of positive real numbers to converge against some real number
- it is necessary that the sequence is bounded,
- it is sufficient that the sequence is monotone decreasing,
- it is necessary and sufficient that it is a Cauchy sequence.
The same statements are expressed by:
- For a sequence
the following is true:
Cauchy convergence criterion
A sequence (an) of real numbers is convergent if and only if for all ε > 0 there is a number N such that |an − am| < ε for all n,m > N.
Root test
A series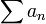 
of (real or complex) numbers an
- is convergent if
![\limsup_{n\to\infty} \sqrt[n]{|a_n|} <1](images/math/d/3/e/d3ee7407bbfdf47988edb99866ef10ae.png)
, and
- is divergent if
![\limsup_{n\to\infty} \sqrt[n]{|a_n|} >1](images/math/4/1/7/417bc94c54e2b369b42046d28d0f4bf1.png)
.
This test is traditionally often referred to as a "criterion" even though
- it does not decide in the case where
![\limsup_{n\to\infty} \sqrt[n]{|a_n|} =1](images/math/7/9/e/79eca472d61c016d82bbc468c28a8f09.png)
,
and therefore is not a true criterion.
Characterization of circles
A circle (in the plane) — more precisely: an arc of a circle — is usually defined as
- a curve such that its points all have the same distance from a given point.
An example of an alternative characterization of these arcs is the following:
- Circles are the plane curves with non-zero constant curvature.
|
Some content on this page may previously have appeared on Citizendium. |
