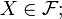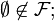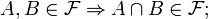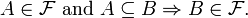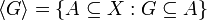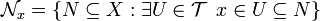Filter (mathematics)
In set theory, a filter is a family of subsets of a given set which has properties generalising those of neighbourhoods in topology.
Formally, a filter on a set X is a subset 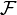 of the power set
of the power set  with the properties:
with the properties:
If G is a nonempty subset of X then the family
is a filter, the principal filter generated by G.
In a topological space 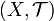 , the neighbourhoods of a point x
, the neighbourhoods of a point x
form a filter, the neighbourhood filter of x.
Filter bases
A base 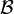 for the filter
for the filter 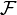 is a non-empty collection of non-empty sets such that the family of subsets of X containing some element of
is a non-empty collection of non-empty sets such that the family of subsets of X containing some element of 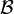 is precisely the filter
is precisely the filter 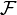 .
.
Ultrafilters
An ultrafilter is a maximal filter: that is, a filter on a set which is not properly contained in any other filter on the set. Equivalently, it is a filter 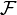 with the property that for any subset
with the property that for any subset 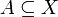 either
either 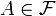 or the complement
or the complement 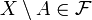 .
.
The principal filter generated by a singleton set {x}, namely, all subsets of X containing x, is an ultrafilter.
| |
Some content on this page may previously have appeared on Citizendium. |