Square root of two
The square root of two, denoted 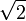 , is the positive number whose square equals 2. It is approximately 1.4142135623730950488016887242097. It provides a typical example of an irrational number.
, is the positive number whose square equals 2. It is approximately 1.4142135623730950488016887242097. It provides a typical example of an irrational number.
In Right Triangles
The square root of two plays an important role in right triangles in that a unit right triangle (where both legs are equal to 1), has a hypotenuse of 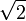 . Thus,
. Thus, 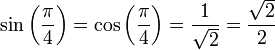 .
.
Proof of Irrationality
There exists a simple proof by contradiction showing that 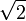 is irrational. This proof is often attributed to Pythagoras. It is an example of a reductio ad absurdum type of proof:
is irrational. This proof is often attributed to Pythagoras. It is an example of a reductio ad absurdum type of proof:
Suppose 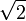 is rational. Then there must exist two numbers,
is rational. Then there must exist two numbers, 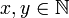 , such that
, such that 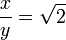 and x and y represent the smallest such integers (i.e., they are mutually prime).
and x and y represent the smallest such integers (i.e., they are mutually prime).
Therefore, 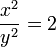 and
and 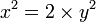 ,
,
Thus, x2 represents an even number; therefore x must also be even. This means that there is an integer k such that 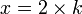 . Inserting it back into our previous equation, we find that
. Inserting it back into our previous equation, we find that 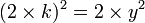
Through simplification, we find that 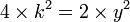 , and then that,
, and then that, 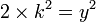 ,
,
Since k is an integer, y2 and therefore also y must also be even. However, if x and y are both even, they share a common factor of 2, making them not mutually prime. And that is a contradiction, so the assumption must be false, and 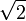 must not be rational.
must not be rational.
| |
Some content on this page may previously have appeared on Citizendium. |