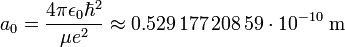Bohr radius
Bohr's theory of the hydrogen atom (1913) predicts the existence of a smallest orbit for the electron circulating the hydrogen nucleus. Today the radius of this orbit is called the Bohr radius. It is usually indicated by a0.
In the old quantum theory of Bohr and Arnold Sommerfeld, as well as in the new quantum theory of Werner Heisenberg and Erwin Schrödinger the radius is given by
where ε0 is the vacuum permittivity (electric constant), 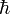 is Planck's reduced constant, μ is the reduced mass of the hydrogen atom (is equal to the electron mass when the proton mass may supposed to be infinite; for the numerical value given this assumption is made) and e is the charge of the electron.
is Planck's reduced constant, μ is the reduced mass of the hydrogen atom (is equal to the electron mass when the proton mass may supposed to be infinite; for the numerical value given this assumption is made) and e is the charge of the electron.
In quantum mechanics, a0 appears as the maximum in the radial distribution associated with the electronic wave function Ψ1s(r) of lowest energy of the hydrogen atom, the 1s atomic orbital. That is, a0 is the position of the maximum in the radial distribution 4πr 2 |Ψ1s(r) |2 and in that sense a0 is a measure for the "size" of the hydrogen atom.