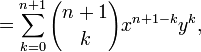Binomial theorem
In elementary algebra, the binomial theorem or the binomial expansion is a mechanism by which expressions of the form (x + y)n can be expanded. It is the identity that states that for any non-negative integer n,
where
is a binomial coefficient. Another useful way of stating it is the following:
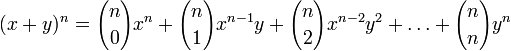
Contents |
[edit] Pascal's triangle
An alternate way to find the binomial coefficients is by using Pascal's triange. The triangle is built from apex down, starting with the number one alone on a row. Each number is equal to the sum of the two numbers directly above it.
n=0 1 n=1 1 1 n=2 1 2 1 n=3 1 3 3 1 n=4 1 4 6 4 1 n=5 1 5 10 10 5 1
Thus, the binomial coefficients for the expression (x + y)4 are 1, 3, 6, 4, and 1.
[edit] Proof
One way to prove this identity is by mathematical induction.
Base case: n = 0
Induction case: Now suppose that it is true for n : 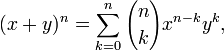 and prove it for n + 1.
and prove it for n + 1.
and the proof is complete.
[edit] Examples
These are the expansions from 0 to 6.
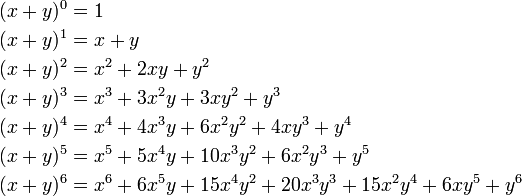
[edit] Newton's binomial theorem
There is also Newton's binomial theorem, proved by Isaac Newton, that goes beyond elementary algebra into mathematical analysis, which expands the same sum (x + y)n as an infinite series when n is not an integer or is not positive.
| |
Some content on this page may previously have appeared on Citizendium. |


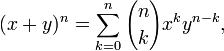
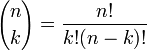
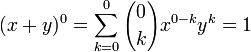
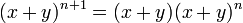
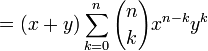
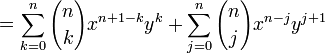
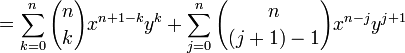
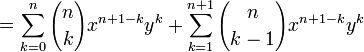
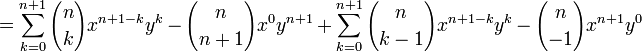
![= \sum_{k=0}^{n+1} \left[ {n \choose k} + {n \choose {k -1}} \right] x^{n+1-k} y^k \,](images/math/1/0/e/10e9e60e7f43b49bc04a157f1f675875.png)