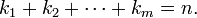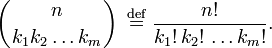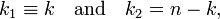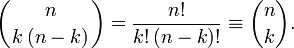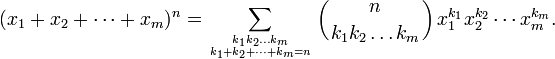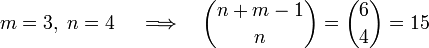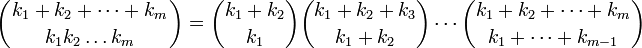Multinomial coefficient
In discrete mathematics, the multinomial coefficient arises as a generalization of the binomial coefficient.
Let k1, k2, ..., km be natural numbers giving a partition of n:
The multinomial coefficient is defined by
For m = 2 we may write:
so that
It follows that the multinomial coefficient is equal to the binomial coefficient for the partition of n into two integer numbers. However, the two coefficients (binomial and multinomial) are notated somewhat differently for m = 2.
The multinomial coefficients arise in the multinomial expansion
The number of terms in this expansion is equal to the binomial coefficient:
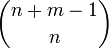
Example. Expand (x + y + z)4:
The 15 terms are the following:
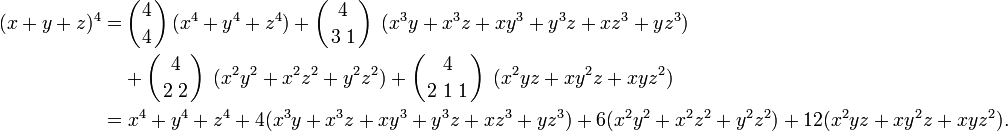
A multinomial coefficient can be expressed in terms of binomial coefficients:
Reference
D. E. Knuth, The Art of Computer Programming, Vol I. Addison-Wesley, Reading Mass (1968) p. 64