Dedekind domain
From Knowino
A Dedekind domain is a Noetherian domain o, integrally closed in its field of fractions, so that every prime ideal is maximal.
These axioms are sufficient for ensuring that every ideal of o that is not (0) or (1) can be written as a finite product of prime ideals in a unique way (up to a permutation of the terms of the product). In fact, this property has a natural extension to the fractional ideals of the field of fractions of o.
This product extends to the set of fractional ideals of the field K = Frac(o) (i.e., the nonzero finitely generated o-submodules of K).
Useful properties
- Every principal ideal domain is a unique factorization domain, but the converse is not true in general. However, these notions are equivalent for Dedekind domains; that is, a Dedekind domain A is a principal ideal domain if and only if it is a unique factorization domain.
- The localization of a Dedekind domain at a non-zero prime ideal is a principal ideal domain, which is either a field or a discrete valuation ring.
Examples
- The ring
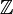 is a Dedekind domain.
is a Dedekind domain.
- Let K be an algebraic number field. Then the integral closure oKof
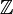 in K is again a Dedekind domain. In fact, if o is a Dedekind domain with field of fractions K, and L / K is a finite extension of K and O is the integral closure of o in L, then O is again a Dedekind domain.
in K is again a Dedekind domain. In fact, if o is a Dedekind domain with field of fractions K, and L / K is a finite extension of K and O is the integral closure of o in L, then O is again a Dedekind domain.
| |
Some content on this page may previously have appeared on Citizendium. |