Separation axioms
From Knowino
Contents |
In topology, separation axioms describe classes of topological spaces according to how well the open sets of the topology distinguish between distinct points.
[edit] Terminology
A neighbourhood of a point x in a topological space X is a set N such that x is in the interior of N; that is, there is an open set U such that 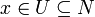 .
A neighbourhood of a set A in X is a set N such that A is contained in the interior of N; that is, there is an open set U such that
.
A neighbourhood of a set A in X is a set N such that A is contained in the interior of N; that is, there is an open set U such that 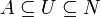 .
.
Subsets U and V are separated in X if U is disjoint from the closure of V and V is disjoint from the closure of U.
A Urysohn function for subsets A and B of X is a continuous function f from X to the real unit interval such that f is 0 on A and 1 on B.
[edit] Axioms
A topological space X is
- T0 if for any two distinct points there is an open set which contains just one
- T1 if for any two points x, y there are open sets U and V such that U contains x but not y, and V contains y but not x
- T2 if any two distinct points have disjoint neighbourhoods
- T2½ if distinct points have disjoint closed neighbourhoods
- T3 if a closed set A and a point x not in A have disjoint neighbourhoods
- T3½ if for any closed set A and point x not in A there is a Urysohn function for A and {x}
- T4 if disjoint closed sets have disjoint neighbourhoods
- T5 if separated sets have disjoint neighbourhoods
- Hausdorff is a synonym for T2
- completely Hausdorff is a synonym for T2½
- regular means T0 and T3
- completely regular means T0 and T3½
- Tychonoff means completely regular and T1
- normal means T0 and T4
- completely normal means T1 and T5
- perfectly normal means: normal and such that every closed set is a Gδ
[edit] Properties
- A space is T1 if and only if each point (singleton) forms a closed set.
- Urysohn's Lemma: if A and B are disjoint closed subsets of a T4 space X, there is a Urysohn function for A and B.
[edit] References
- Steen, Lynn Arthur & J. Arthur Jr. Seebach (1978), Counterexamples in Topology, Berlin, New York: Springer-Verlag, ISBN 0-387-90312-7
| |
Some content on this page may previously have appeared on Citizendium. |

