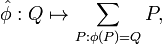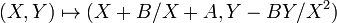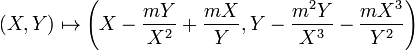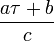Isogeny
In algebraic geometry, an isogeny between abelian varieties is a rational map which is also a group homomorphism, with finite kernel.
Contents |
Elliptic curves
As 1-dimensional abelian varieties, elliptic curves provide a convenient introduction to the theory. If 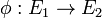 is a non-trivial rational map which maps the zero of E1 to the zero of E1, then it is necessarily a group homomorphism. The kernel of φ is a proper subvariety of E1 and hence a finite set of order d, the degree of φ. Conversely, every finite subgroup of E1 is the kernel of some isogeny.
is a non-trivial rational map which maps the zero of E1 to the zero of E1, then it is necessarily a group homomorphism. The kernel of φ is a proper subvariety of E1 and hence a finite set of order d, the degree of φ. Conversely, every finite subgroup of E1 is the kernel of some isogeny.
There is a dual isogeny 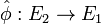 defined by
defined by
the sum being taken on E1 of the d points on the fibre over Q. This is indeed an isogeny, and the composite 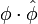 is just multiplication by d.
is just multiplication by d.
The curves E1 and E2 are said to be isogenous: this is an equivalence relation on isomorphism classes of elliptic curves.
Examples
Let E1 be an elliptic curve over a field K of characteristic not 2 or 3 in Weierstrass form.
Degree 2
A subgroup of order 2 on E1 must be of the form 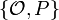 where P = (e,0) with e being a root of the cubic in X. Translating so that e=0 and the curve has equation Y2 = X3 + AX2 + BX, the map
where P = (e,0) with e being a root of the cubic in X. Translating so that e=0 and the curve has equation Y2 = X3 + AX2 + BX, the map
is an isogeny from E1 to the isogenous curve E2 with equation Y2 = X3 − 2AX2 + (A2 − 4B)X.
Degree 3
A subgroup of order 3 must be of the form 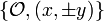 where x is
in K but y need not be. We shall assume that
where x is
in K but y need not be. We shall assume that 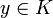 (by taking a quadratic twist if necessary). Translating, we can put E in the form Y2 + XY + mY = X3. The map
(by taking a quadratic twist if necessary). Translating, we can put E in the form Y2 + XY + mY = X3. The map
is an isogeny from E1 to the isogenous curve E2 with equation Y2 + XY + 3mY = X3 − 6mX − (m + 9m2).
Elliptic curves over the complex numbers
An elliptic curve over the complex numbers is isomorphic to a quotient of the complex numbers by some lattice. If E1 = C/L1, and L1 is a sublattice of L2 of index d, then E2 = C/L2 is an isogenous curve. Representing the homothety class of a lattice by a point τ in the upper half-plane, the isogenous curves correspond to the lattices with moduli
with a.c = d and b=0,1,...,c-1.
Elliptic curves over finite fields
Isogenous elliptic curves over a finite field have the same number of points (although not necessarily the same group structure). The converse is also true: this is the Honda-Tate theorem.
References
- J.W.S. Cassels (1991). Lectures on Elliptic Curves. Cambridge University Press, 58-65. ISBN 0-521-42530-1.
- Dale Husemöller (1987). Elliptic curves. Springer-Verlag, 91-96,163. ISBN 0-387-96371-5.
- Joseph H. Silverman (1986). The Arithmetic of Elliptic Curves. Springer-Verlag, 70-79,84-90. ISBN 0-387-96203-4.
| |
Some content on this page may previously have appeared on Citizendium. |