Metric space
In mathematics, a metric space is, roughly speaking, an abstract mathematical structure that generalizes the notion of a Euclidean space 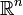 which has been equipped with the Euclidean distance, to more general classes of sets such as a set of functions. The notion of a metric space consists of two components, a set and a metric in that set. In a metric space, the metric replaces the Euclidean distance as a notion of "distance" between any pair of elements in its associated set (for example, as an abstract distance between two functions in a set of functions) and induces a topology in the set called the metric topology.
which has been equipped with the Euclidean distance, to more general classes of sets such as a set of functions. The notion of a metric space consists of two components, a set and a metric in that set. In a metric space, the metric replaces the Euclidean distance as a notion of "distance" between any pair of elements in its associated set (for example, as an abstract distance between two functions in a set of functions) and induces a topology in the set called the metric topology.
The theory of metric spaces includes the following topics: isometric embeddings and universal metric spaces (in the sense of isometric embeddings); metric maps (which do not increase distances); the category of metric spaces and metric maps, and its subcategories; injective metric spaces and related notions; special classes of metric spaces like strongly convex spaces; metric generalizations of the notions of differential geometry; metric properties of the metric spaces which appear in other branches of mathematics (e.g. Banach spaces, in particular Hilbert spaces).
The topic of metric spaces can be attractive both to children and to research mathematicians. Certain deeper directions in the theory of metric spaces are closely related to the approximation theory.
Every simple graph can be viewed as a metric space (in more than one way). Thus formally the theory of simple graphs can be considered as a special chapter of the theory of metric spaces. Indeed, as a rule, the notions of the theory of simple graphs can be rephrased in the language of metric spaces (possibly in more than one way).
Contents |
Metric in a set
Let 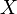 be an arbitrary set. A metric
be an arbitrary set. A metric 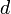 on
on 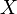 is a function
is a function 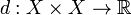 with the following properties:
with the following properties:
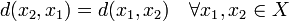 (symmetry)
(symmetry)
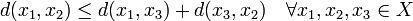 (triangular inequality)
(triangular inequality)
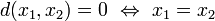
It follows from the above three axioms of a metric (also called distance function) that:
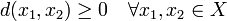 (non-negativity)
(non-negativity)
Definition of metric space
A metric space is an ordered pair 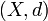 where
where 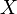 is a set and
is a set and 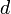 is a metric on
is a metric on 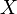 .
.
For shorthand, a metric space 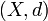 is usually written simply as
is usually written simply as 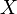 once the metric
once the metric 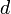 has been defined or is understood.
has been defined or is understood.
Metric topology
A metric on a set 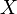 induces a particular topology on
induces a particular topology on 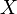 called the metric topology. For any
called the metric topology. For any 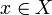 , let the open ball
, let the open ball 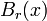 of radius
of radius 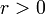 around the point
around the point 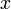 be defined as
be defined as 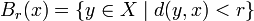 . Define the collection
. Define the collection  of subsets of
of subsets of 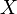 (meaning that
(meaning that 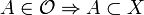 ) consisting of the empty set
) consisting of the empty set 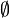 and all sets of the form:
and all sets of the form:
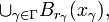
where 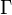 is an arbitrary index set (can be uncountable) and
is an arbitrary index set (can be uncountable) and 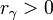 and
and  for all
for all 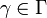 . Then the set
. Then the set 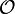 satisfies all the requirements to be a topology on
satisfies all the requirements to be a topology on 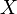 and is said to be the topology induced by the metric
and is said to be the topology induced by the metric 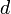 . Any topology induced by a metric is said to be a metric topology.
. Any topology induced by a metric is said to be a metric topology.
Examples
- The "canonical" example of a metric space, and indeed what motivated the general definition of such a space, is the Euclidean space
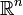 endowed with the Euclidean distance
endowed with the Euclidean distance 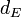 defined by
defined by 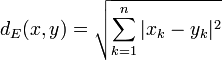 for all
for all 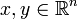 .
.
- Consider the set
![C[a,b]\,](images/math/1/2/d/12dc259d5b0ea6bb39558142e2a0f27d.png) of all real valued continuous functions on the interval
of all real valued continuous functions on the interval ![[a,b]\subset \mathbb{R}](images/math/a/5/4/a54f51b0256823149bb71b71fddcdb70.png) with
with 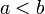 . Define the function
. Define the function ![d:C[a,b] \times C[a,b] \rightarrow \mathbb{R}](images/math/7/d/5/7d55a0e97994bb368160fb3b29c7792f.png) by
by ![d(f,g)=\max_{x \in [a,b]}|f(x)-g(x)|](images/math/0/9/b/09b29b98fd168d82058a4753109cec82.png) for all
for all ![f,g \in C[a,b]](images/math/c/3/2/c32a7f3be1c6d1ac68012750519ec9d3.png) . This function
. This function 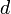 is a metric on
is a metric on ![C[a,b]\,](images/math/1/2/d/12dc259d5b0ea6bb39558142e2a0f27d.png) and induces a topology on
and induces a topology on ![C[a,b]\,](images/math/1/2/d/12dc259d5b0ea6bb39558142e2a0f27d.png) often known as the norm topology or uniform topology.
often known as the norm topology or uniform topology.
- Let
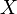 be any nonempty set. The discrete metric on
be any nonempty set. The discrete metric on 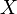 is defined as
is defined as 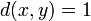 if
if 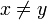 and
and 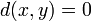 otherwise. In this case the induced topology is the discrete topology, in which every set is open.
otherwise. In this case the induced topology is the discrete topology, in which every set is open.
Mappings
A mapping f from a metric space (X,d) to another (Y,e) is an isometry if it is distance-preserving: that is
A mapping f from a metric space (X,d) to another (Y,e) is continuous at x in X if for all real ε > 0 there exists δ > 0 such that
and continuous if it is continuous at every point of X.
If we let Bd(x,r) denote the open ball of radius r round x in X, and similarly Be(y,r) denote the open ball of radius r round y in Y, we can express these conditions in terms of the pull-back 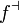
See also
References
1. K. Yosida, Functional Analysis (6 ed.), ser. Classics in Mathematics, Berlin, Heidelberg, New York: Springer-Verlag, 1980
| |
Some content on this page may previously have appeared on Citizendium. |
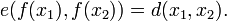
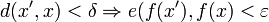
![f^{\dashv}[B_e(f(x),\varepsilon)] \supseteq B_d(x,\delta) . \,](images/math/0/7/2/072c8cb2314fab9a3d08b2c4b7bd99aa.png)