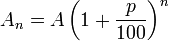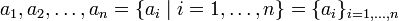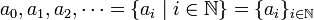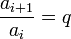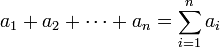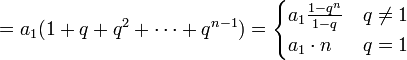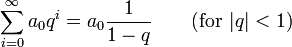Geometric sequence
A geometric sequence (or geometric progression) is a (finite or infinite) sequence of (real or complex) numbers such that the quotient (or ratio) of consecutive elements is the same for every pair.
In finance, compound interest generates a geometric sequence.
Examples
Examples for geometric sequences are
- 3,6,12,24,48,96 (finite, length 6: 6 elements, quotient 2)
- 1, − 2,4, − 8 (finite, length 4: 4 elements, quotient −2)
-
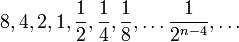 (infinite, quotient
(infinite, quotient  )
)
-
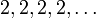 (infinite, quotient 1)
(infinite, quotient 1)
-
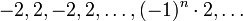 (infinite, quotient −1)
(infinite, quotient −1)
-
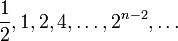 (infinite, quotient 2)
(infinite, quotient 2)
-
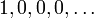 (infinite, quotient 0) (See General form below)
(infinite, quotient 0) (See General form below)
Application in finance
The computation of compound interest leads to a geometric series:
When an initial amount A is deposited at an interest rate of p percent per time period then the value An of the deposit after n time-periods is given by
i.e., the values A=A0, A1, A2, A3, ... form a geometric sequence with quotient q = 1+(p/100).
Mathematical notation
A finite sequence
or an infinite sequence
is called geometric sequence if
for all indices i where q is a number independent of i. (The indices need not start at 0 or 1.)
General form
Thus, the elements of a geometric sequence can be written as
- ai = a1qi − 1
Remark: This form includes two cases not covered by the initial definition depending on the quotient:
- a1 = 0 , q arbitrary: 0, 0•q = 0, 0, 0, ...
- q = 0 : a1, 0•a1 = 0, 0, 0, ...
(The initial definition does not cover these two cases because there is no division by 0.)
Sum
The sum (of the elements) of a finite geometric sequence is
The sum of an infinite geometric sequence is a geometric series:
| |
Some content on this page may previously have appeared on Citizendium. |