Percentile
Percentiles are statistical parameters which describe the distribution of a (real) value in a population (or a sample). Roughly speaking, the k-th percentile separates the smallest k percent of values from the largest (100-k) percent.
Special percentiles are the median (50th percentile), the quartiles (25th and 75th percentile), the quintiles (20th, 40th, 60th and 80th percentile), and the deciles (the k-th decile is the (10k)-th percentile). Percentiles are special cases of quantiles: The k-th percentile is the same as the (k/100)-quantile.
Definition
The value x is k-th percentile (for a given k = 1,2,...,99) if
In this definition, P is a probability distribution on the real numbers. It may be obtained either
- from a (theoretical) probability measure (such as the normal or Poisson distribution), or
- from a finite population where it expresses the probability of a random element to have the property,
i.e., it is the relative frequency of elements with this property (number of elements with the property divided by the size of the population),or - from a sample of size N where it also is the relative frequency which is used to estimate the corresponding percentile for the population from which it was taken.
Special cases
For most standard continuous distributions (like the normal distribution) the k-th percentile x is uniquely determined by
In the general case (e.g., for discrete distributions, or for finite samples) it may happen that the separating value has positive probability:
or that there is a gap in the range of the variable such that, for two distinct x1 < x2, equality holds:
Then every value in the (closed) interval between the smallest and the largest such value
is a k-th percentile.
Examples
The following examples illustrate this:
- Take a sample of 101 values, ordered according to their size:
-
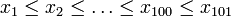 .
.
-
- Then the unique k-th percentile is xk + 1.
- If there are only 100 values
-
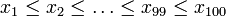 .
.
-
- Then any value between xk and xk + 1 is a k-th percentile.
Example from the praxis:
Educational institutions (i.e. universities, schools...) frequently report admission test scores in terms of percentiles.
For instance, assume that a candidate obtained 85 on her verbal test.
The question is: How did this student compared to all other students?
If she is told that her score correspond to the 80th percentile,
we know that approximately 80% of the other candidates scored lower than she
and that approximately 20% of the students had a higher score than she had.
| |
Some content on this page may previously have appeared on Citizendium. |
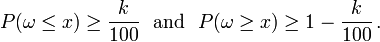
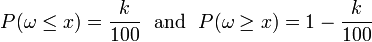
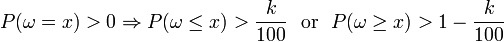
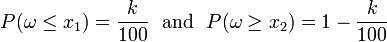
![\left [ \min \left\{ x \Bigl\vert P(\omega\le x) = {k\over100} \right\},
\max \left\{ x \Bigl\vert P(\omega\ge x) = 1-{k\over100} \right\} \right]](images/math/7/5/b/75b119956493d20a54738dcd8f2e0e46.png)